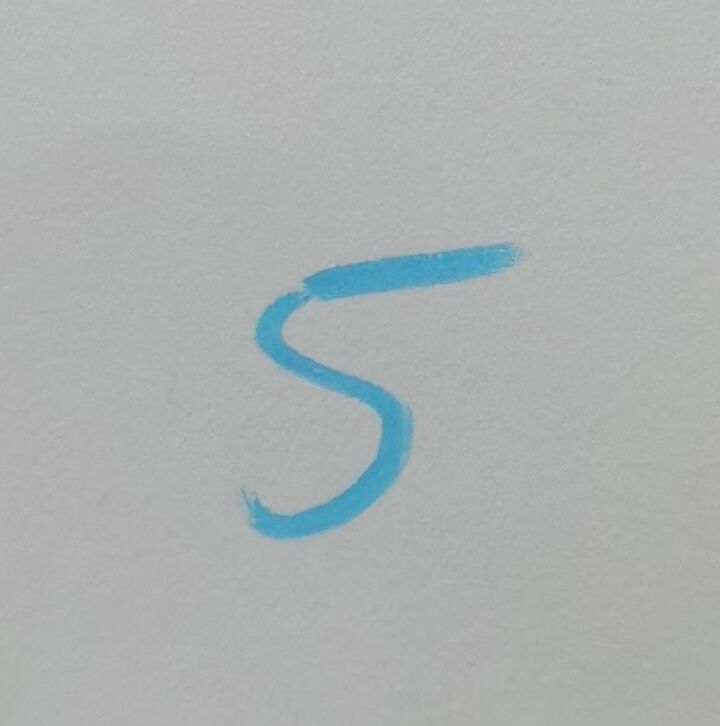KNN算法简介
k近邻法(k-nearest
neighbor,k-NN)属于监督学习中的分类算法,是机器学习中最简单的算法之一,同时也是最常用的分类算法之一。这篇文章将会基于numpy手动实现KNN,在此之后,将会利用sklearn实现的KNN完成数字识别。
KNN需要数据标准化。
算法原理
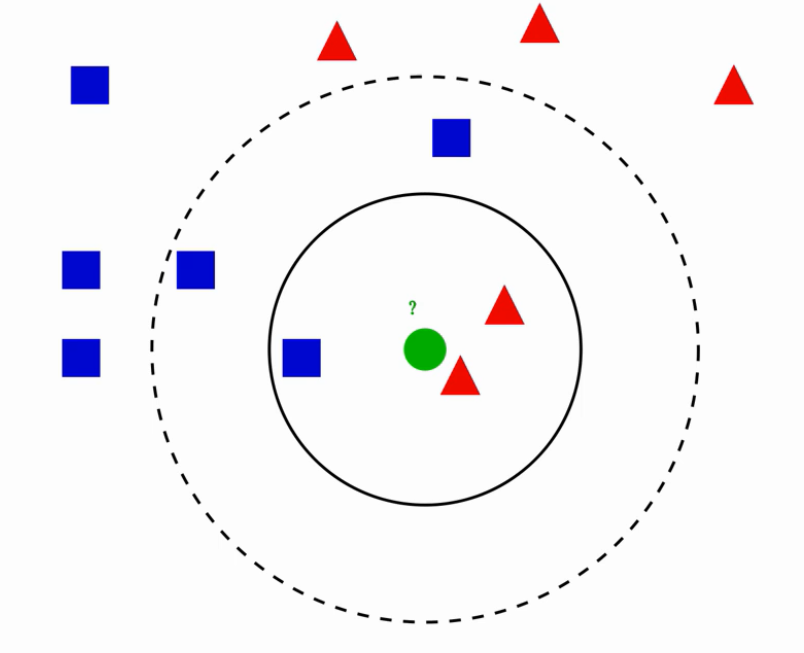
KNN不同于其他机器学习算法,它不需要训练过程 ,当使用该算法预测一个新的值时,它会根据距离最近的K个点的类型来判断自己的类型:K个点中哪个类型多就属于哪个类型。
例:
当K等于3时,根据上述规则可得预测为红类;
当K等于5时,根据上述规则可得预测为蓝类。
基本流程
计算新数据与每一个已知样本的距离
按距离从小到大排序
选出距离最小的K个点
通过这K个点的分类决策新数据所属类别
KNN算法的三要素
根据上面的例子,可以看出不同K的选择对预测结果有较大影响。实验表明,K值越小,越容易发生过拟合;K值越大,越容易发生欠拟合。除K值的选择 外,影响KNN算法的还有距离度量 、分类决策规则 。
分类决策规则一般采用多数表决,即最近的K个样本中哪个种类多就属于哪一类。
距离度量
有同维度特征空间向量\(\vec A =
(a_1,a_2,...,a_n),\vec B = (b_1,b_2,...,b_n)\) ,则\(\vec A\) ,\(\vec
B\) 的\(L_P\) 距离为:
\(L_p(\vec A,\vec B) =
(\sum_{i=1}^n|a_i-b_i|^p)^{\frac 1 p}\)
曼哈顿距离(P=1):\(L_1 =
\sum_{i=1}^n|a_i-b_i|\)
欧式距离(P=2):\(L_2 =
\sqrt{\sum_{i=1}^n|a_i-b_i|^2}\)
切比雪夫距离(\(P=\infty\) ):\(L_{\infty} =
max(|a_1-b_1|,|a_2-b_2|,...,|a_n-b_n|)\)
一般采用欧式距离作为距离度量。
K值选择-交叉验证
交叉验证简介:将原始数据集可以分为训练集、验证集、测试集。利用训练集和验证集测试模型好坏的方法叫做交叉验证。注:交叉验证是没有用到测试集的!如果用测试集进行交叉验证,会导致预测结果乐观化。
通过交叉验证方法可以得到最合适的K值。
KNN算法的优缺点以及改进方法
优点:
原理简单,便于实现。
KNN是惰性模型,不需要训练。
预测效果好。
对异常值不敏感。
缺点:通过KNN算法原理可以得知,如果要预测一个新数据,需要将它和每一个样本都计算一次距离,然后排序,选出最小的K个样本进行决策。那么预测一次的时间复杂度为\(O(n)\) ,时间复杂度较高。并且需要将所有样本都储存在内存,空间复杂度较高,即对内存要求较高。所以KNN算法的缺点主要是:
效率比较低,运行时间可能比较长。
对内存要求较高。
KNN适用于数据集较小的分类。对于数据集较大的可使用神经网络进行分类。
KNN改进算法介绍
这里不会说明各算法的原理与实现,只会简单介绍,参考文章:盘点高效的KNN实现算法-技术圈
(proginn.com)
上述提到的均是KNN的线性扫描 实现方法,即暴力法。通过分析,可知线性扫描不适用于数据规模较大的数据集。
实际上,KNN的实现方法高大10种,下面将介绍几种改进方法。
KD树
KD树是一种树形结构 存储算法。
适用范围:
KD树在特征维度小于20时效率最高 ,一般适用于训练样本数远大于空间维数时的k近邻搜索。当空间维数接近训练实例数时,效率会迅速下降,几乎接近线形扫描。
Ball树
ball树是KD树的一种改良算法。
Annoy
Annoy,全称“A pproximate N earest N eighbors O h Y eah”,是一种适合实际应用的快速相似查找算法。
Annoy 同样通过建立一个二叉树,使得每个点查找时间复杂度是O(log
n)。和KD树不同的是,Annoy没有对k维特征进行切分。
HNSW
HNSW(H ierarchcal N avigable S mall W orld
graphs)是基于图存储 的数据结构。
上述四种算法中,Annoy和HNSW是可以在实际业务中落地的算法。
KNN算法手动实现完成鸢尾花分类
主体部分
详细解释都写代码里了,因为主体部分实在太短了没必要分开写,就直接写在一个模块了:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 import numpy as npimport operatordef run_KNN (X,X_train,y_train,K ): ''' :param X: 需要预测的数据集 :param X_train: X训练集 :param y_train: Y训练集 :param K: K个最近 :return: 预测集 ''' dataSize = X_train.shape[0 ] y_predict = [] for x in X: diff = np.tile(x,(dataSize,1 )) - X_train squaredDist = np.sum (diff**2 ,axis=1 ) distance = squaredDist ** 0.5 nearIds = distance.argsort() classesCount = {} for i in range (K): y = y_train[nearIds[i]] classesCount[y] = classesCount.get(y,0 )+1 sortClassesCount = sorted (classesCount.items(),key=operator.itemgetter(1 ),reverse=True ) y_predict.append(sortClassesCount[0 ][0 ]) return y_predict
到这里,就已经手动实现了KNN算法,可以拿来预测类别了,确实很简单。
但我们还需要利用交叉验证集选择最好的K,本来想借助sklearn的交叉验证,但是对我们自己手写的KNN好像不太好用,所以还是自己写一个简易的吧。
不过像拆分训练集和计算Score这种事就交给sklearn吧。
交叉验证选择最适K值
注意,交叉验证集不能涉及到测试集!
这里用多次交叉验证计算score取均值:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 import matplotlib.pyplot as pltfrom sklearn.model_selection import train_test_splitfrom sklearn.metrics import f1_scoredef chooseK (X_train_old,y_train_old,K = 10 ,C = 5 ): ''' :param X_train_old: 原训练特征集 :param y_train_old: 原训练目标集 :param K: 最大K :param C: 计算次数 :return: 最好的K值 ''' scores = [0 ] for k in range (1 ,K+1 ): score = 0 for j in range (1 ,C+1 ): X_train, X_check, y_train, y_check = train_test_split(X_train_old, y_train_old, train_size=0.6 ) y_predict = run_KNN(X_check,X_train,y_train,k) score = score + f1_score(y_check, y_predict, average='weighted' ) score = score/(C) scores.append(score) scores = np.array(scores) bestK = scores.argmax() plt_KScore(scores,K,bestK) return bestK def plt_KScore (scores,K,bestK ): k_range = range (1 ,K+1 ) plt.plot(k_range,scores[1 :]) plt.scatter(bestK,scores[bestK],marker='o' ,c='red' ) plt.xlabel('Value of K in KNN' ) plt.ylabel('Score' ) plt.show()'Score' ) plt.show()
下面将测试交叉验证集选择K值。
这里使用sklearn自带的鸢尾花数据集,标准化之前的文章已经手动实现过,这里直接用sklearn自带。
导入数据和预处理
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import timefrom sklearn import datasetsfrom sklearn.preprocessing import StandardScalerif __name__ == '__main__' : iris = datasets.load_iris() dataSet = iris.data target = iris.target X_train, X_test, y_train, y_test = train_test_split(dataSet,target, train_size=0.7 , random_state=10 ) scaler = StandardScaler() X_train = scaler.fit_transform(X_train) X_test = scaler.transform(X_test)
现在开始测试交叉验证集选择K:
1 2 3 4 5 6 start = time.time() K = chooseK(X_train,y_train,50 ) print (f"bestK is {K} " )end = time.time() print (f"run time is {end-start} " )
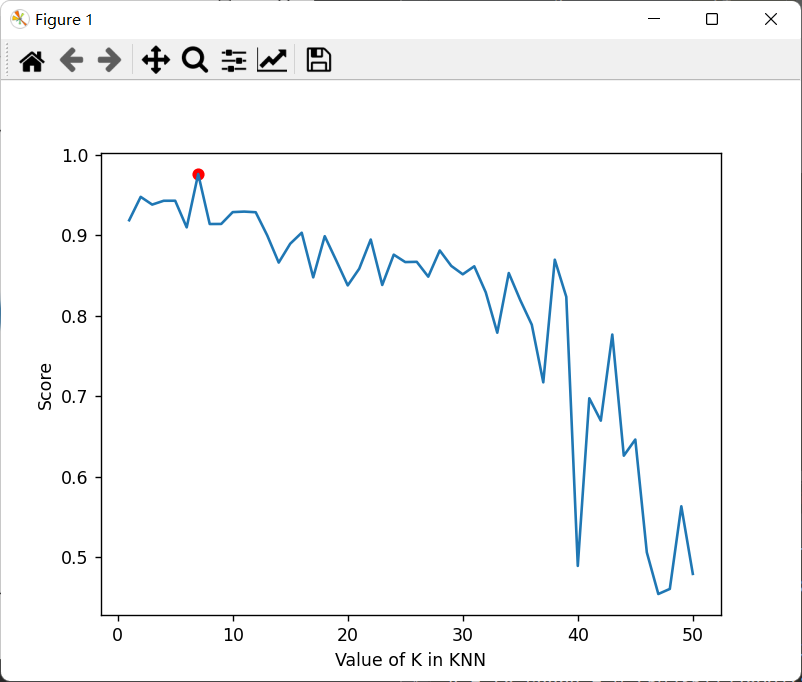
结果:
1 2 bestK is 7 run time is 2.0105364322662354
实际上会发现每次计算出来的“Best
K”都不一样,不过都在那几个值跳动,这是因为在分割测试集和验证集时没有设置随机种子的原因。
现在,让我们用最好的K值来测试分类效果吧!
1 2 3 4 5 6 7 8 start = time.time() best_K = chooseK(X_train,y_train,50 ) print (f"bestK is {best_K} " )y_predict = run_KNN(X_test,X_train,y_train,best_K) score = f1_score(y_test, y_predict, average='weighted' ) print (f"predict score is {score} " )end = time.time() print (f"run time is {end-start} " )
结果:
1 2 3 bestK is 4 predict score is 0.9778242192035296 run time is 0.400089502334594704
可以看出bestK和上一次算的不一样,不过最后分类的结果还是非常好的。
利用Sklearn实现KNN完成鸢尾花分类
关于sklearn封装的KNN的参数说明详细请参考文章: KNN算法详解及实现__dingzhen的博客-CSDN博客_knn
读懂每一个需要的参数很很很重要!!一定要去看参数说明 。
sklearn的KNN实现方式包括了之前提到的线性扫描 、KDTree 和ballTree ,没有规定特定参数时它会自己选则实现方法。详细说明都在链接里了。
这次我们用Sklearn封装的KNN来完成上面提到的例子,即鸢尾花分类。同样也用了交叉验证寻找最佳K值。
详见代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 import timeimport numpy as npimport matplotlib.pyplot as pltfrom sklearn.metrics import f1_scorefrom sklearn.model_selection import cross_val_score, train_test_splitfrom sklearn.neighbors import KNeighborsClassifierfrom sklearn import datasetsfrom sklearn.preprocessing import StandardScalerdef findBestK (X_train,y_train,max_k = 50 ): k_scores = [0 ] for k in range (1 ,max_k+1 ): Knn = KNeighborsClassifier(n_neighbors=k) scores = cross_val_score(Knn,X_train,y_train,cv=5 ,scoring='f1_weighted' ) k_scores.append(scores.mean()) k_scores = np.array(k_scores) bestK = k_scores.argmax() plt_KScore(k_scores,max_k,bestK) return bestK def plt_KScore (scores,K,bestK ): k_range = range (1 ,K+1 ) plt.plot(k_range,scores[1 :]) plt.scatter(bestK,scores[bestK],marker='o' ,c='red' ) plt.xlabel('Value of K in KNN' ) plt.ylabel('Score' ) plt.show() if __name__ == '__main__' : iris = datasets.load_iris() dataSet = iris.data target = iris.target X_train, X_test, y_train, y_test = train_test_split(dataSet,target, train_size=0.7 , random_state=10 ) scaler = StandardScaler() X_train = scaler.fit_transform(X_train) X_test = scaler.transform(X_test) start = time.time() best_K = findBestK(X_train,y_train) print (f"best_k is {best_K} " ) model = KNeighborsClassifier(n_neighbors=best_K) model.fit(X_train,y_train) y_predict = model.predict(X_test) score = f1_score(y_test, y_predict, average='weighted' ) print (f"predict score is {score} " ) end = time.time() print (f"run time is {end - start} " )
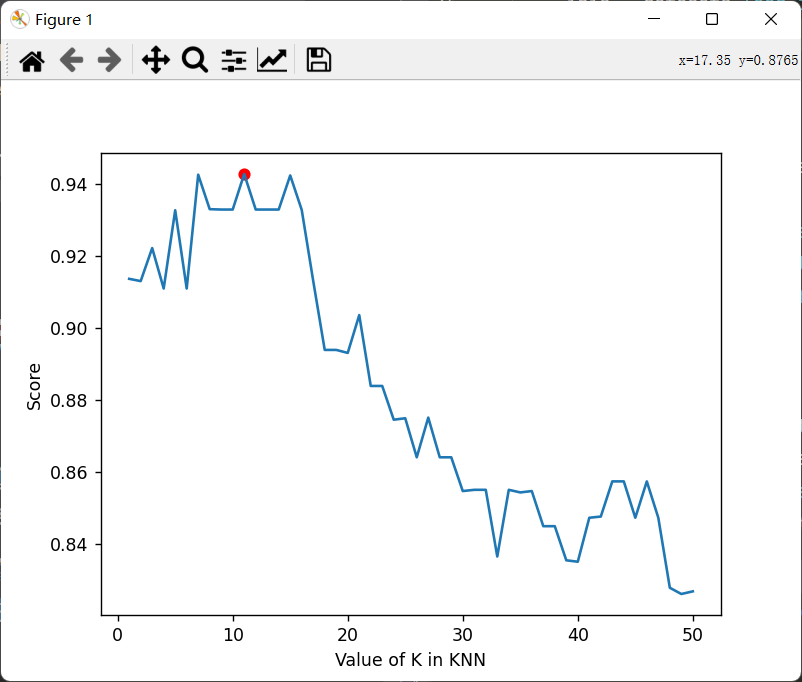
交叉验证集选择K:
最终结果:
1 2 3 best_k is 11 predict score is 0.9778242192035296 run time is 0.7521629333496094
通过自己实现的KNN与sklearn实现的KNN对比,发现:
自己实现的KNN寻找到的最佳K值不固定,而sklearn每次寻找的最佳K值都一样。导致自己实现的KNN最佳K值不固定的原因是拆分数据集和验证集时每次的随机种子不固定。偶尔有几次自己算出来的结果和sklearn算出来的结果完全一致。
使用同种实现方式(即线性扫描实现KNN)时,sklearn用的时间比自己实现的要长那么一点点,暂时不清楚原因。
利用Sklearn的KNN完成手写数字识别
到此为止,你已经学会了如何自己实现KNN算法,并且取得了不错的分类效果。现在我们用sklrean封装好的KNN来完成一些有趣的事吧!
手写数据识别是计算机视觉方面的入门级图像识别,一般都是用神经网络实现的,不过我们可以使用KNN来完成数据规模比较小的手写数字识别。
在此之前,请确保你已经安装tensorflow和keras,我们的数据集将来自keras。
当然也可以自己找数据。
需要的包:
1 2 3 4 import numpy as npimport matplotlib.pyplot as pltfrom keras.datasets import mnistfrom sklearn.neighbors import KNeighborsClassifier
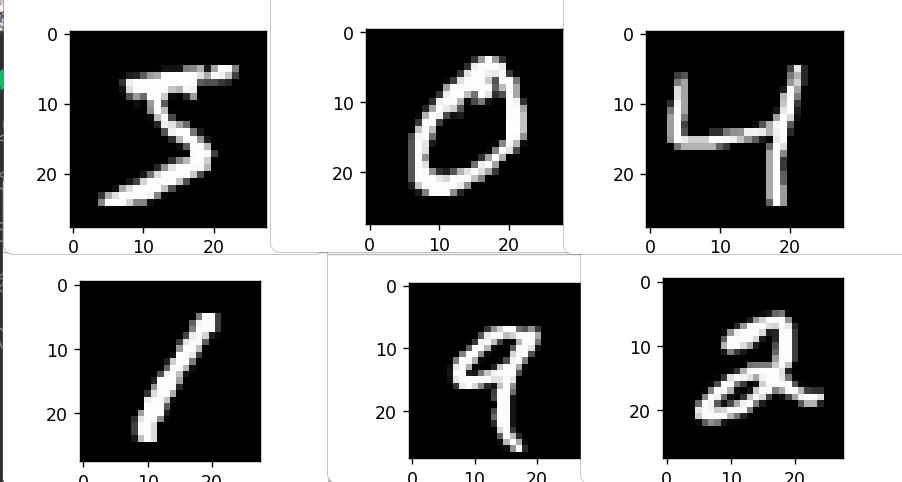
导入数据并查看数字图像
1 2 3 4 5 6 7 8 if __name__ == '__main__' : (X_train,y_train),(X_test,y_test) = mnist.load_data() for i in range (6 ): plt.figure() plt.imshow(X_train[i],cmap='gray' ) plt.show()
查看X_train训练集的形状:
看得出是个三维的,大概意思是60000张图片,\(28\times
28\) 像素,且是灰色(因为如果是彩色,应该是\(28\times28\times3\) )
要用KNN算法,需要先将三维转化为二维矩阵\((60000,28 \times 28)\)
,每一行代表一张图片,共60000张。
数据预处理
1 2 3 4 5 6 X_train = X_train.reshape([-1 ,28 *28 ]) X_test = X_test.reshape([-1 ,28 *28 ]) X_train /= 255 X_test /= 255
选择最佳K值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 def findBestK (X_train,y_train,max_k = 50 ): k_scores = [0 ] for k in range (1 ,max_k+1 ): print (f"{k} time" ) Knn = KNeighborsClassifier(n_neighbors=k) scores = cross_val_score(Knn,X_train,y_train,cv=5 ,scoring='f1_weighted' ) k_scores.append(scores.mean()) k_scores = np.array(k_scores) bestK = k_scores.argmax() return bestK def plt_KScore (scores,K,bestK ): k_range = range (1 ,K+1 ) plt.plot(k_range,scores[1 :]) plt.scatter(bestK,scores[bestK],marker='o' ,c='red' ) plt.xlabel('Value of K in KNN' ) plt.ylabel('Score' ) plt.show()
1 2 3 4 5 6 7 8 9 10 11 start = time.time() best_K = findBestK(X_train[:10000 ], y_train[:10000 ]) print (f"best_k is {best_K} " )end = time.time() print (f"run time is {end - start} " )
结果:
1 2 best_k is 4 run time is 54.95526051521301
这一步太慢了!!整整耗时55秒。强烈建议不要进行,如果需要最佳K值,上面已经算出来了。
训练模型,测试模型得分
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 start = time.time() model = KNeighborsClassifier(n_neighbors=4 ) model.fit(X_train,y_train) y_predict = model.predict(X_test) score = f1_score(y_test, y_predict, average='weighted' ) print (f"predict score is {score} " ) end = time.time() print (f"run time is {end - start} " )
结果:
1 2 predict score is 0.9681286795453637 run time is 7.25964617729187
可以看出模型很不错!到此为止,使用KNN进行手写数字识别可以说完成了。
但是,作为一个合格的玩具,它还没完。
接下来是可选内容:把它变成可以玩的玩具!
完成手写数字识别玩具
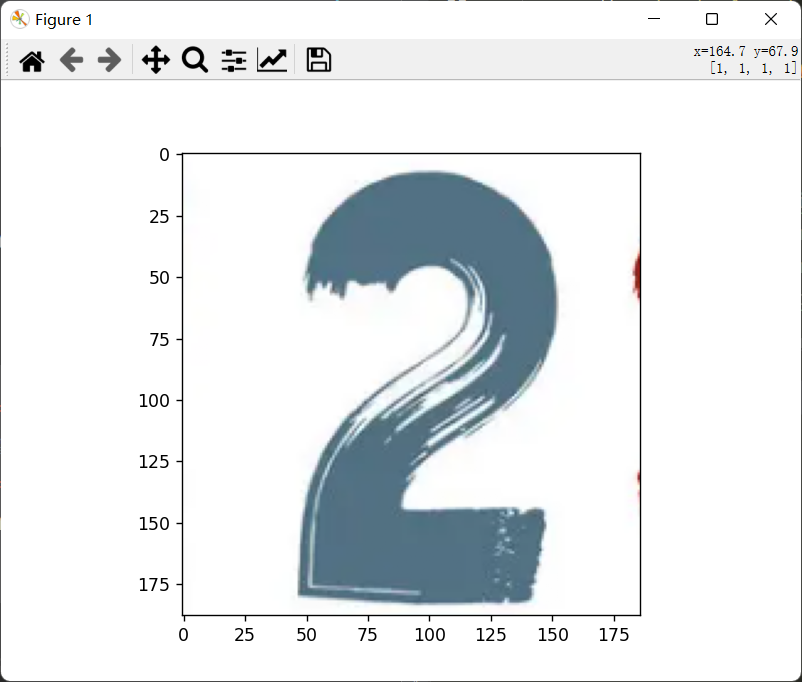
现在假设你拿到了这样一张图片:
很显然,它是彩色的,但是我们之前训练用的图片是灰色的,而且,中间是白色的,像这样:
另外,两张像素可能不一样,前者像素不确定,后者为\(28\times
28\) 所以我们需要先把图片做一些预处理:
将彩色图片变为灰色图片(即将三图层变为单图层)
将图片像素压缩为\(28\times28\)
可以将图片二值化(即0和255),可能识别效果会更好。
图片预处理
接下来会用到opencv-python包,但是注意高版本的tensorflow和opencv-python可能出现不兼容的问题。最开始我用的tensorflow2.9.0,对应的numpy为1.23。但是安装opencv后会自动把numpy降为1.16,导致tensorflow用不了。所以这里可能需要切换一下环境。
我用的环境:tensorflow2.6.0+opencv4.5.5+numpy1.19.5
tensorflow版本降低后,数据集的导入可能会发生变化。
改变导入形式:
1 2 3 4 5 6 7 8 import cv2import timeimport numpy as npimport matplotlib.pyplot as pltfrom tensorflow.keras.datasets import mnistfrom sklearn.metrics import f1_scorefrom sklearn.model_selection import cross_val_scorefrom sklearn.neighbors import KNeighborsClassifier
将彩色图片以灰度图片导入
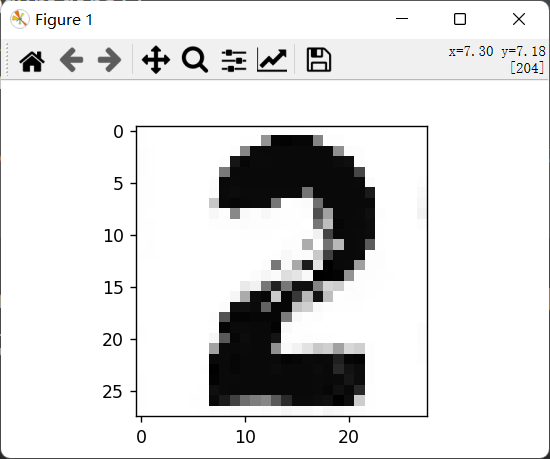
查看原图片:
1 2 3 4 5 path = 'number1.png' img1 = plt.imread(path) plt.imshow(img1) plt.show()
以灰度图片导入并查看
1 2 3 4 5 6 7 imgOriginal = cv2.imread(path,0 ) img = np.asarray(imgOriginal) print (f"before resize shape is:{img.shape} " )img = cv2.resize(img,(28 ,28 )) print (f"after resize shape is:{img.shape} " )plt.imshow(img,cmap='Greys_r' ) plt.show()
如果不加cmap='Greys_r',matplotlib会把这张灰色图片由低维(1维)映射到高维(3维),然后以彩色图片的形式展出,这显然不符合我们这里的需求。
输出:
1 2 before resize shape is :(188 , 186 ) after resize shape is :(28 , 28 )
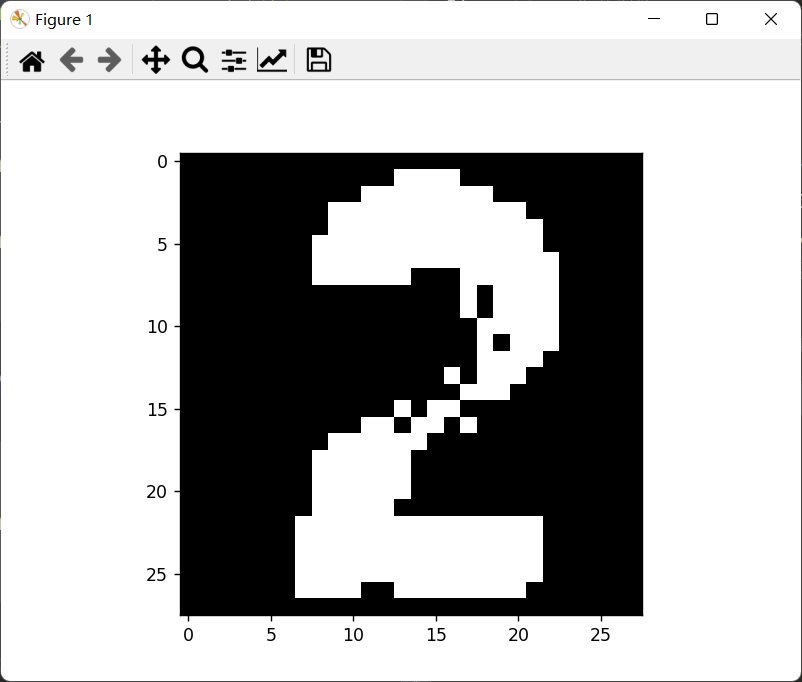
黑白颠倒以及二值化
我们的样本数据集为黑底白字,所以需要将这张图片也要变为黑底白字。同时我们可以将其二值化,变为黑白图像:
这里的二值化只是简单实现了下,还有更好的二值化方法,以后再学了。
1 2 3 4 5 6 7 8 9 10 11 12 def Binarization (img,Reverse = False ): ''' :param img: :param Reverse: 是否黑白颠倒 :return: ''' if Reverse == False : img = np.where(img > 160 ,255 ,0 ) else : img = np.where(img > 160 ,0 ,255 ) return img
现在将图片二值化:
1 2 3 img = Binarization(img,Reverse = True ) plt.imshow(img, cmap='Greys_r' ) plt.show()
最后不要忘记了归一化和转化矩阵:
1 2 X = img/255.0 X = X.reshape(-1 ,28 *28 )
使用模型识别手写数字
1 2 predict = model.predict(X) print (f"手写数字识别为:{predict[0 ]} " )
结果:
完整代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 import cv2import timeimport numpy as npimport matplotlib.pyplot as pltfrom tensorflow.keras.datasets import mnistfrom sklearn.metrics import f1_scorefrom sklearn.model_selection import cross_val_scorefrom sklearn.neighbors import KNeighborsClassifierdef findBestK (X_train,y_train,max_k = 50 ): k_scores = [0 ] for k in range (1 ,max_k+1 ): print (f"{k} time" ) Knn = KNeighborsClassifier(n_neighbors=k) scores = cross_val_score(Knn,X_train,y_train,cv=5 ,scoring='f1_weighted' ) k_scores.append(scores.mean()) k_scores = np.array(k_scores) bestK = k_scores.argmax() return bestK def plt_KScore (scores,K,bestK ): k_range = range (1 ,K+1 ) plt.plot(k_range,scores[1 :]) plt.scatter(bestK,scores[bestK],marker='o' ,c='red' ) plt.xlabel('Value of K in KNN' ) plt.ylabel('Score' ) plt.show() def cal_score (model,X_test,y_test ): y_predict = model.predict(X_test) score = f1_score(y_test, y_predict, average='weighted' ) print (f"predict score is {score} " ) def Binarization (img,Reverse ): ''' :param img: :param Reverse: 是否黑白颠倒 :return: ''' if Reverse == False : img = np.where(img > 160 ,255 ,0 ) else : img = np.where(img > 160 ,0 ,255 ) return img def identification_number (path,model = None ,Reverse = False ): imgOriginal = cv2.imread(path,0 ) img = np.asarray(imgOriginal) img = cv2.resize(img,(28 ,28 )) img = Binarization(img,Reverse) X = img/255.0 X = X.reshape(-1 ,28 *28 ) predict = model.predict(X) print (f"手写数字识别为:{predict[0 ]} " ) if __name__ == '__main__' : (X_train,y_train),(X_test,y_test) = mnist.load_data() X_train = X_train /255.0 X_test = X_test /255.0 X_train = X_train.reshape([-1 ,28 *28 ]) X_test = X_test.reshape([-1 ,28 *28 ]) model = KNeighborsClassifier(n_neighbors=4 ) model.fit(X_train,y_train) img_path = 'number1.png' identification_number(img_path,model,Reverse=True )
对模型的总结和评价
实际上因为没有用神经网络来做这个手写数字识别模型,加上二值化写的比较草率,它对于真实手写数字识别效果并没有预料的好。待会儿会举两个识别自己手写数字的例子。
在二值化时阈值的选择影响比较大,最开始阈值设置的200,结果自己手写的数字二值化后变成了一片白或黑色。后来调整到160-170左右,感觉比较合适。
咱也是第一次做手写数字识别玩具,整个过程还是很有意思的。
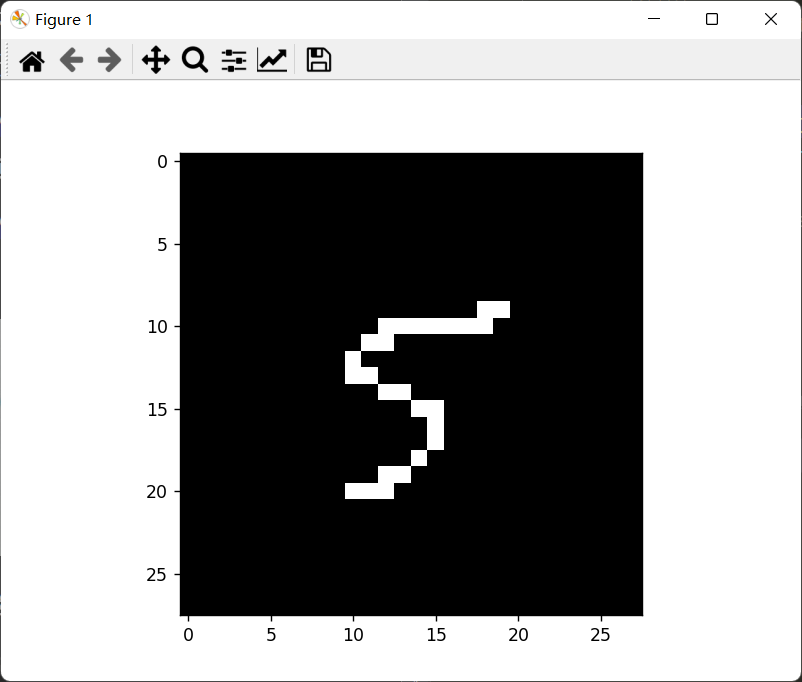
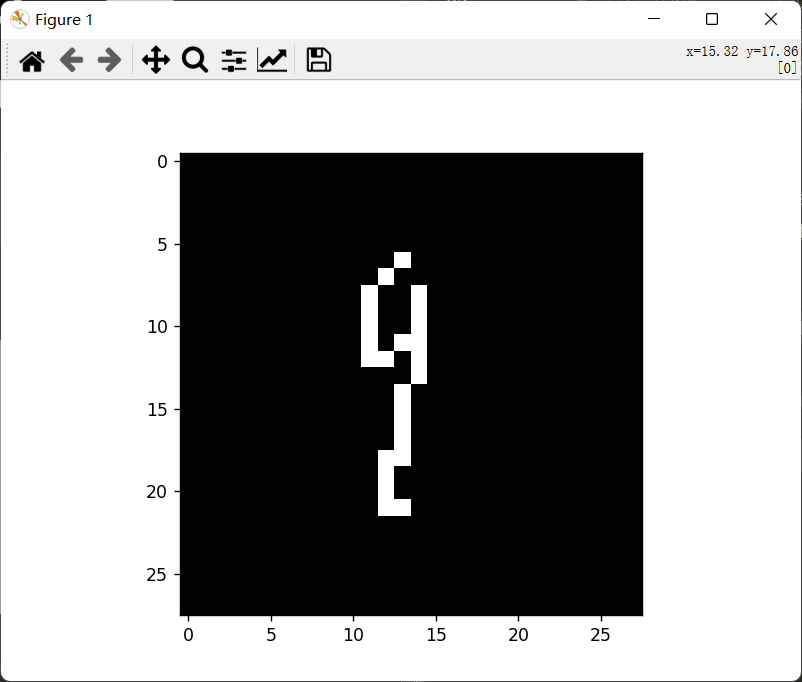
自己写的数字:
二值化和预测结果:
识别失败: