机器学习笔记1——一元线性回归

前言：本系列为机器学习的学习笔记，参考教程链接：

(强推|双字)2022吴恩达机器学习Deeplearning.ai课程

观点不一定完全正确，欢迎指出错误的地方。

什么是线性回归模型？

回归分析是研究自变量与因变量之间数量变化关系的一种分析方法，它主要是通过因变量Y与影响它的自变量\(X_{i}\)（i=1,2,3…）之间的回归模型，衡量自变量\(X_{i}\)对因变量Y的影响能力的，进而可以用来预测因变量Y的发展趋势。线性回归模型指因变量和自变量呈直线型关系的模型，是回归分析中最常用且最简单的方法，线性归回模型又分为一元线性回归模型和多元回归模型。

---

一元线性回归模型

一元线性回归模型即自变量只有一个的线

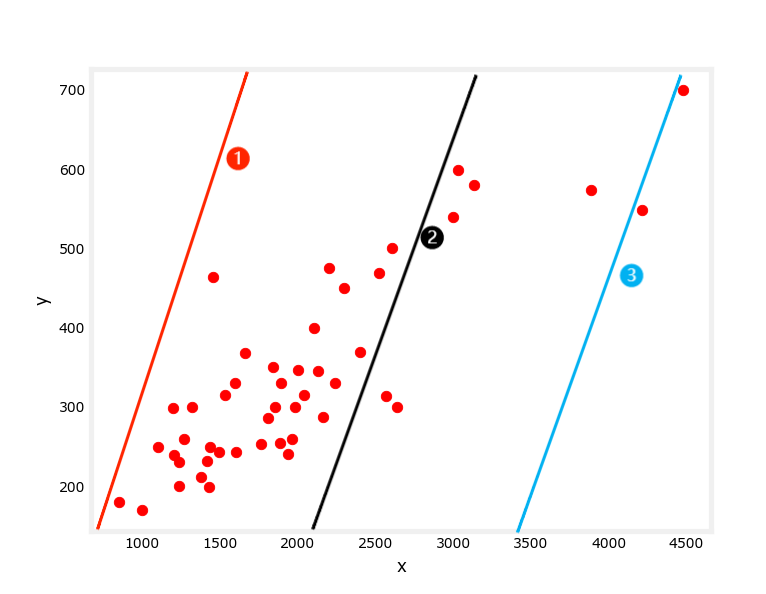
问题引入：

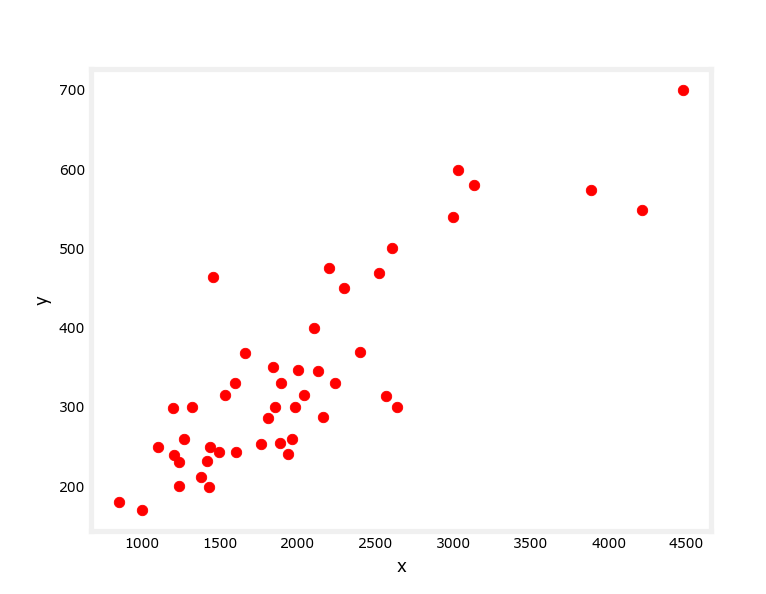
已知上图数据集，其中，X为自变量，Y为因变量，请预测当X为5000时Y的取值。

问题解析：

因为自变量只有一个，即让你模拟一个\(f_{w,b}(x)=wx+b\),使该函数与上图自变量与应变量的变化趋势尽量满足，\(f_{w,b}(x)\)即一元线性回归函数，再用计算出的回归函数去预测值即可。难点在于，这里的w和b都是未知数，我们要做的就是推断出最合适的w和b。

代价函数（损失函数）：

如何判断w和b是否合适，我们引入了代价函数。代价函数用于判断整体来看，每个点（Y）实际值与估计值的差距大小。

这里先随便画一条线。

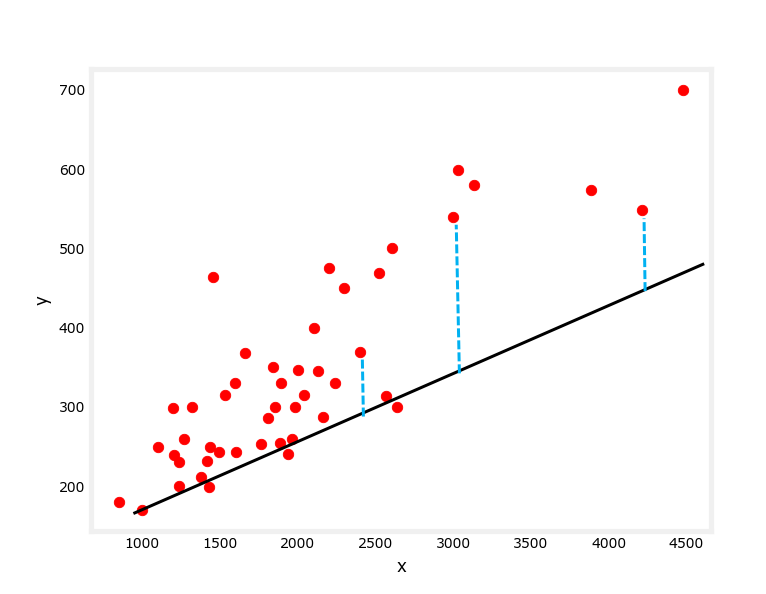
令模拟出来的自变量对应应变量的值为\(\hat{y}\),即\(\hat{y} = f_{w,b}(x)\),则代价函数为：

\(J(w,b) =\frac{1}{2m}\sum_{i=0}^{m-1}{(\hat{y}_{i}-y_{i})^2} = \frac{1}{2m}\sum_{i=0}^{m-1}{(f_{w,b}(x_{i})-y_{i})^2}\)

其中，m为训练集样例数，第一个点下标为0。这里除以2是方便后续计算。

代价函数的图像

我们先将\(f_{w,b}(x)\)简化为\(f_{w}(x) = wx\),那么\(J(w) = \frac{1}{2m}\sum_{i=0}^{m-1}{(wx_{i}-y_{i})^2}\)

此时\(J(w)\)的图像为一个凸函数

对应的\(f_w(x)\)模拟情况：

当我们将\(f_{w,b}(x)\)简化为\(f_{b}(x) = x+b\),此时\(J(b)\)的图像也是一个凸函数，我们姑且借用\(J(w)\)的图像，不过变量变为了b:

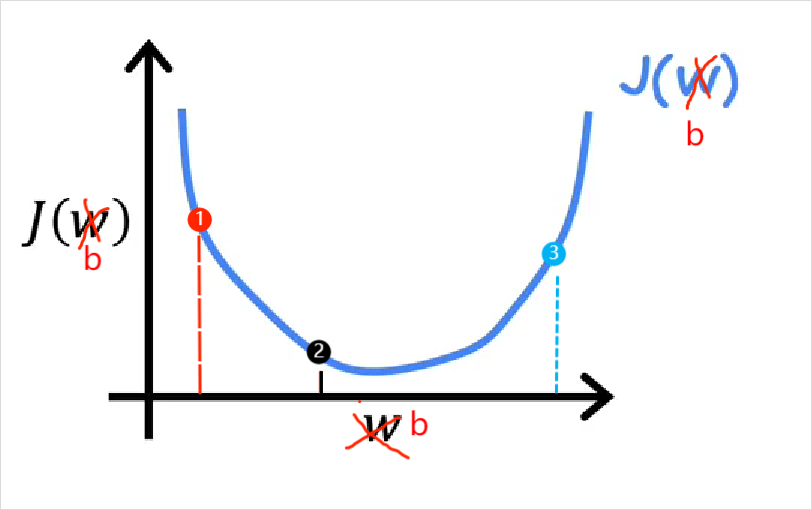
对应的\(f_{b}(x)\)模拟情况：

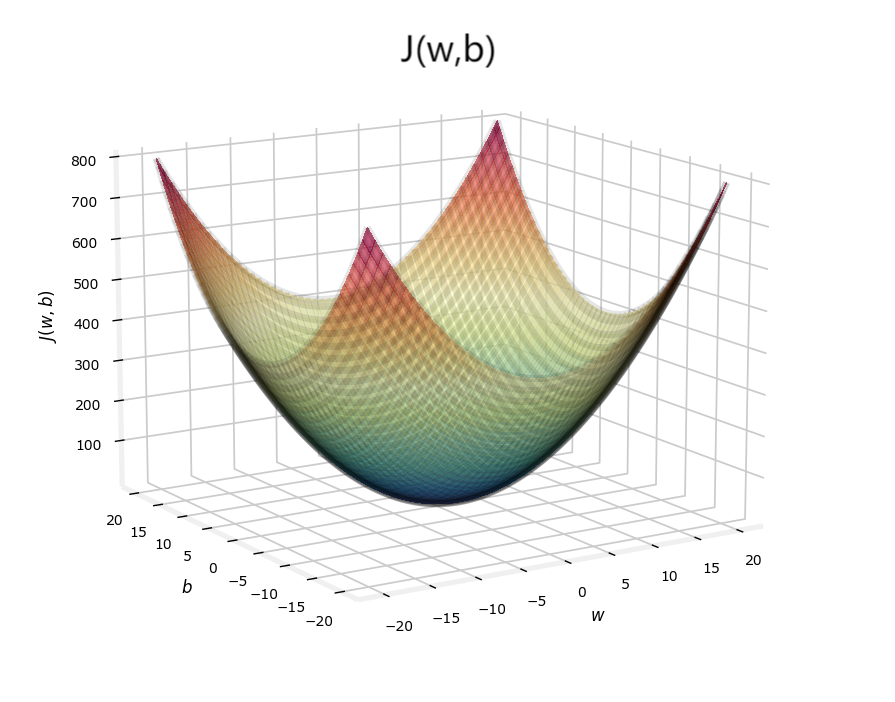
现在将\(J(w)\)和\(J(b)\)合在一起，\(J(w,b)\)便是一个三维碗装图像：

注：图中的w和b并不对应上面的例子，只是大致图像！

代价函数计算出的值越小，说明模拟值与实际值差距越小，则w，b越合适，回归函数模拟的越好。所以，当代价函数值最小时，w和b最合适。

于是问题转化为了：求w和b使得\(J(w,b)\)能取到极小值。

为什么不是最小而是极小值？

这与之后要用到的算法（梯度下降法）有关，梯度下降法只能求到极小值。不过梯度下降法常用于求凸函数的极小值，而凸函数只有一个极小值，所以通常求得的是最小值。这里举个非凸函数的例子，此时用梯度下降法不一定能求得最优解。

梯度下降算法

梯度下降算法并不只用于求解线性回归问题。

梯度算法在讲座中被描述为：假设你站在一个山坡上，你想最快下降到你四周最低的山谷。

即选择一个基点，以四周斜率绝对值最大的方向下降，直到下降到极小值点（此时斜率为0）停止。我们认为这个极小值点对应的w和b即为所求，一般我们选择\((0,0)\)作为基点，即w和b开始为\((0,0)\)，不过实际上基点怎么选都可以。

梯度下降算法公式（对于一元线性回归模型）：

重复以下行为直到收敛：

\(w = w - a\frac{\partial J(w,b)}{\partial w}\)

\(b = b - a\frac{\partial J(w,b)}{\partial b}\)

其中，\(a\)被称为学习率。之后会讨论学习率\(a\)的选择。

注意：w和b应该同时更新！（会在代码块详细说明）

\(\frac{\partial J(w,b)}{\partial w} = \frac{1}{m}\sum_{i=0}^{m-1}{(f_{w,b}(x_{i})-y_{i})}x_{i}\)

\(\frac{\partial J(w,b)}{\partial w} = \frac{1}{m}\sum_{i=0}^{m-1}{(f_{w,b}(x_{i})-y_{i})}\)

(之前代价函数除个2就是为了这里化简)

学习率a的选择

如果\(a\)很小，那么每一步都走的很小，收敛过程就会很慢。

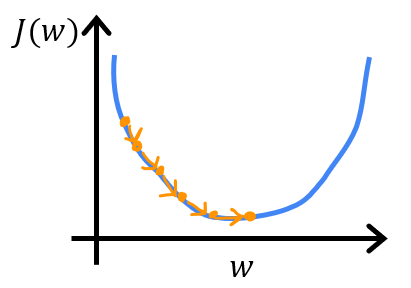
如果\(a\)很大，\(J(w,b)\)可能不会每次迭代都下降，可能错过最佳点，甚至导致发散。

关于学习率的设置有许多种方法，这里不做专门讨论（其实是还没学到），姑且采用网上查到的一种简单的方法：在运行梯度下降法的时候会尝试一系列学习率的取值：...0.001, 0.003，0.01, 0.03，0.1, 0.3，1....尽量以三倍增长，直到找到一个合适的学习率。

关于梯度下降每一步的变化

梯度下降每一步并不是相等的，因为每一次迭代时，偏导数都会不断变化。在学习率选择合适的情况下，大概可以得到以下的每一步梯度变化图像。x轴为迭代次数，y轴为梯度。

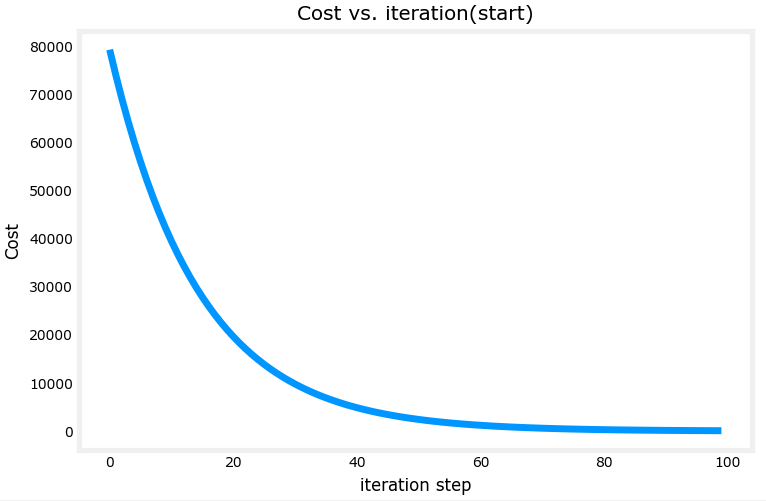
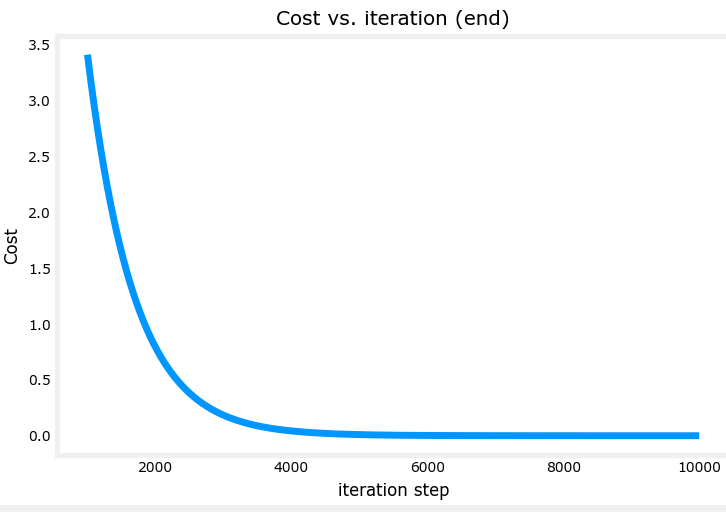
可以看到最开始梯度很大，到后来慢慢接近于0。

补充：

这里解释下为什么非凸函数中找到的不一定是最优解：

我们选择1和2分别作为起点，可能到达两个极小值点，我们无法判断找到的极小值点是否是全局最小值。当然凸函数只有一个极值点，所以对于凸函数，不存在这个问题。

代码部分 - 案例实现

数据

2104.000000,1600.000000,2400.000000,1416.000000,3000.000000,1985.000000,1534.000000,1427.000000,1380.000000,1494.000000,1940.000000,2000.000000,1890.000000,4478.000000,1268.000000,2300.000000,1320.000000,1236.000000,2609.000000,3031.000000,1767.000000,1888.000000,1604.000000,1962.000000,3890.000000,1100.000000,1458.000000,2526.000000,2200.000000,2637.000000,1839.000000,1000.000000,2040.000000,3137.000000,1811.000000,1437.000000,1239.000000,2132.000000,4215.000000,2162.000000,1664.000000,2238.000000,2567.000000,1200.000000,852.000000,1852.000000,1203.000000
399.899994,329.899994,369.000000,232.000000,539.900024,299.899994,314.899994,198.998993,212.000000,242.500000,239.998993,347.000000,329.998993,699.900024,259.899994,449.899994,299.899994,199.899994,499.997986,599.000000,252.899994,255.000000,242.899994,259.899994,573.900024,249.899994,464.500000,469.000000,475.000000,299.899994,349.899994,169.899994,314.899994,579.900024,285.899994,249.899994,229.899994,345.000000,549.000000,287.000000,368.500000,329.899994,314.000000,299.000000,179.899994,299.899994,239.500000

导入数据并绘制初始图

import numpy as np
import matplotlib.pyplot as plt

data = np.loadtxt('test.txt',dtype=np.float32,delimiter=',')
x_train = data[0]
y_train = data[1]
plt.scatter(x_train,y_train,marker='o',c='r') # marker 将样式设置为叉，c将颜色设置为红色
plt.ylabel('y')
plt.xlabel('x')
plt.show()

梯度产生函数

对应公式：

sum_dw = \(\frac{\partial J(w,b)}{\partial w} = \frac{1}{m}\sum_{i=0}^{m-1}{(f_{w,b}(x_{i})-y_{i})}x_i\)

sum_db = \(\frac{\partial J(w,b)}{\partial w} = \frac{1}{m}\sum_{i=0}^{m-1}{(f_{w,b}(x_{i})-y_{i})}\)

# 产生梯度函数
def compute_gradient(x,y,w,b):
    '''
    参数:
        x: x训练集
        y: y训练集
        w,b: 模型参数
    返回值:
        sum_dw: 代价函数对w的偏导数
        sum_db: 代价函数对d的偏导数
    '''

    m = x.shape[0] # 训练样例个数
    sum_dw = 0
    sum_db = 0

    for i in range(m):
        f_wb = w*x[i]+b
        dw_i = (f_wb - y[i])*x[i]
        db_i = f_wb - y[i]
        sum_dw += dw_i
        sum_db += db_i

    sum_dw = sum_dw / m
    sum_db = sum_db / m
    return sum_dw,sum_db

梯度迭代函数

对应公式：

重复以下行为直到收敛：

\(w = w - a\frac{\partial J(w,b)}{\partial w}\)

\(b = b - a\frac{\partial J(w,b)}{\partial b}\)

注：代码中是让他迭代一定次数而并非以收敛为结束判断条件。这是因为当迭代次数足够大，也无限接近收敛了。

# 梯度迭代函数(计算w和b)
def gradient_descent(x,y,init_w,init_b,alpha,num_iters):
    '''
    参数说明:
        x: x训练集
        y: y训练集
        init_w: w初始值
        init_b: b初始值
        alpha: 学习率
        num_iters: 迭代次数
    return:
        w,b:最终找到的w和b
    '''
    w = init_w
    b = init_b

    for i in range(num_iters):
        # 产生梯度
        sum_dw,sum_db = compute_gradient(x, y, w, b)
        # 同时更新w和b
        w = w - alpha*sum_dw
        b = b - alpha*sum_db

    return w,b

代价函数

对应公式：

\(J(w,b) =\frac{1}{2m}\sum_{i=0}^{m-1}{(\hat{y}*{i}-y*{i})^2} = \frac{1}{2m}\sum_{i=0}^{m-1}{(f_{w,b}(x_{i})-y_{i})^2}\)

这里只用于检验结果。

 # 代价函数
def compute_cost(x, y, w, b):
    m = x.shape[0]
    cost = 0

    for i in range(m):
        f_wb = w * x[i] + b
        cost = cost + (f_wb - y[i]) ** 2
    total_cost = 1 / (2 * m) * cost

    return total_cost

绘图和预测

if __name__ == '__main__':

    data = np.loadtxt('test.txt', dtype=np.float32, delimiter=',')
    x_train = data[0]
    y_train = data[1]
    plt.scatter(x_train, y_train, marker='o', c='r')  # marker 将样式设置为叉，c将颜色设置为红色
    plt.ylabel('y')
    plt.xlabel('x')
    # plt.show()

    init_m = 0
    init_b = 0
    # 一些梯度下降的设置
    iterations = 100000
    tmp_alpha = 0.000000095
    w,b = gradient_descent(x_train,y_train,init_m,init_b,tmp_alpha,iterations)
    print(f"线性回归函数为:f(x) = {w}x + {b}")
    print(f"此时代价函数为:{compute_cost(x_train,y_train,w,b)}")
    print(f"预测当x = 5000是，y的值为:{w*5000+b}")
    x = np.linspace(0,5000,100)
    y = w*x+b
    plt.plot(x,y)
    plt.show()

在设置学习率alpha时，如果大了会报错，过小模拟出来的图像差距过大，这里尝试了许多次选了一个自认为比较合适的值。

结果