前言

早在写逻辑回归二分类时就提到过多分类的问题，时隔两个月终于可以把当初这个坑填上了。softmax本应该属于深度学习的笔记，但归为机器学习的笔记，也没什么不妥。好了，闲话不多说。

本篇为softmax多分类器的原理与公式详细推导，关于softmax的具体代码实现和应用将在下一章说明。

softmax多分类器简介

softmax多分类器，一种基于softmax函数的分类器，它可以预测一个样本属于每个样本的概率。softmax一般用于神经网络的输出层，叫做softmax层。

不过不必担心，本篇文章对神经网络没有要求，即使没学过神经网络，也可以学会softmax，并在下一篇文章中学会自己实现softmax代码并完成一个具体的训练和预测示例。

如何利用softmax对样本进行分类

问题引入

如何使用训练集训练一个基于softmax函数的多分类模型，并使用该模型对测试集进行预测？

好吧，这个问题引入写的有点草率了，想了一会儿没啥好写的，就是多分类问题。

明确变量与集合

为了在接下来的推导过程中不搞混各变量的含义，我们需要先明确涉及的变量和集合。

设样本集含有N个样本,令样本集为X,则$X = \{x^1,x^2,x^3...,x^N\}$。注意这里使用的上标，这样写是为了后续方便表示样本的特征。
设任意一个样本含有M个特征，令任意一个样本为$x$,则$x = (x_1,x_2,x_3,...,x_M)$。则第i个样本的第j个特征表示为$x_j^i$。
设样本集共分为K类。记分类集为C,则$C = \{c_1,c_2,...,c_K\}$。
设样本集对应的label集为Y,每一个样本对应一个y,则$Y=\{y_1,y_2,y_3,..,y_N\}$。其中，$y_i$ 的值为$0 \sim K-1$ 中的一个整数。

进一步处理

对label向量化

回顾二分类问题，样本的label要么是0，要么是1。现在变成多分类了，那么样本的label就变成了$0 \sim K-1$ 中任意一个整数。这就不便于我们计算了，所以需要将label进行向量化：

若第i个样本属于第K个分类，即$y_i=c_k$。那么对其进行向量化后： \[ y_i = (0,...,1,...,0) \] 仅在第K-1的位置上值为1，其他位置均为0。

示例

假设共有5个分类，样本$x^i$ 属于第3类，则： \[ y_i = (0,0,1,0,0) \]

对样本特征进行加权组合

在进入softmax层之前，不得不提到特征的加权组合。在神经网络中，这一步的处理其实叫做隐藏层，不过这里就不对隐藏层做拓展了。

为了使softmax拥有一套完整的流程，我们这里对样本特征进行最简单的线性加权组合：

现在有任意一个样本$x = (x_1,x_2,x_3,...,x_M)$ 。$x_i$表示该样本的第$i$个特征。令 \[ z_k = w_k^Tx+b_k = (\sum_{i=1}^Mw_{k,i}x_i)+b_k \] 现在多出了几个参数，下面对它们进行说明：

$z$：对样本$x$的特征进行线性加权组合后得到的输出，$z = (z_1,z_2,...,z_K)$ 。有几个分类就有就有几个$z_k$。
$z_k$：表示对样本的特征进行权值向量为$w_k$ 的线性变换后得到的值，为标量。
$w_k$：第k个权值向量，维度与$x$一样，$(1,N)$。

将$b_k$放在$w_k$ 里：
只需要将$w_k$加一列，即$w_k = (...,b_k)$，
然后再往$x$加一列，即$x = (...,1)$ 。
就可以将$z_k$ 的表达式变为:$z_k = w_k^Tx$

图示（不含$b_k$的情况）：

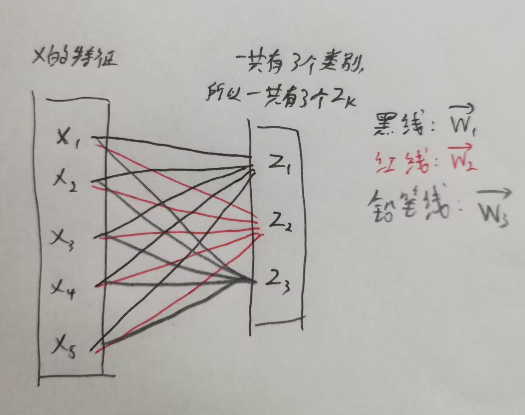
softmax激活函数

激活函数也是神经网络里的称呼，直接叫softmax函数也没问题。

简单来说，softmax预测分类是作用在$z_k$ 上的，这也是为什么之前我们需要对样本特征进行加权组合得到$z_k$。接下来给出公式： \[ a_k = P(y=c_k|x,\theta) = \frac{e^{z_k}}{\sum_{i=1}^Ke^{z_i}},k = 0,1,...,K-1 \]

稍微解释一下这个公式：在模型参数$\theta$固定，且样本已知的情况下，该样本属于第K个分类的概率等于后面那一坨公式。(本文中$\theta$即各权值向量$w_k$)

通过softmax激活函数得到各分类预测概率

将一个样本对应的$a_k$ 全部算出来，这些$a_k$ 就是该样本属于各分类的预测概率。

示例

假设一个样本$x$的特征进行加权组合后得到的$z$为： \[ z = (0.6,1.1,-1.5,1.2,3.2,-1.1) \] 经过softmax激活后： \[ a = (0.055,0.090,0.0067,0.10,0.74,010) \] 比如其中的0.74表示：在已知权值$w$ 的情况下，某一个样本$x$ 属于第5个分类的概率为0.74。

那么如果这是在做测试集的测试，根据“属于谁的概率最大就选谁”的原则，我们可以说x的预测分类为第5个分类，即$label = 4$ 。不过在训练集训练模型时，我们只求到x属于每个类别的概率。

在神经网络中，将上述过程描述为神经网络的正向传播。

总结softmax的正向传播流程

固定模型参数$\theta$ ,在本篇文章中，$\theta$ 即各权值向量$w_k$。
对于一个样本$x = (x_1,x_2,...,x_M)$，先对它的特征做加权组合得到$z = (z_1,..,z_K)$。在本篇文章中，我们仅做了一次线性加权组合。而在神经网络中，可能会对x的特征做多次变换，即隐藏层不止一层。
对$z$ 进行softmax激活得到$a = (a_1,...a_K)$，$a_k$ 表示样本x属于第k类的概率。

引出新的问题

我们进行正向传播时，是在模型参数$\theta$ 已知的情况下进行。而我们现在已知的只有训练集，怎么根据训练集得到这个模型参数$\theta$ 呢？

答案是迭代。我们可以随机初始化模型参数$\theta$，然后通过某种算法一轮一轮的更新$\theta$ ,直到$\theta$ 收敛。

在softmax分类器中，我们使用梯度下降算法对$\theta$进行优化。关于梯度下降算法请见相关文章【1】，在这里就不多说了。

softmax损失函数

损失函数之前的文章已经提到过N次了，不过这里还是说一下。损失函数是用来衡量label预测值和真实值之间的某种差距的函数。常见的损失函数有0-1损失函数、对数损失函数、平方损失函数等等。每种模型需要选择的损失函数不同。如果损失函数选择不当，会对优化过程造成很大影响，详情请见相关文章【2】。

损失函数和代价函数的区别

说来惭愧，我一直都没真正搞清楚损失函数和代价函数的区别，所以之前写文章可能存在这两个词汇混用的问题。这次专门区分一下两者的区别。

损失函数

损失函数（Loss Function ）是定义在单个样本上的，描述单个样本的label预测值与真实值的某种差距。一般记为$L(\hat y,y)$ 。

代价函数

代价函数（Cost Function ）是定义在整个训练集上的，是所有样本误差的平均，也就是损失函数的平均。一般记为$J(...)$。“...”指代的一般为模型未知参数，有许多种写法。 \[ J(...) = \frac{1}{N}\sum_{i=0}^{N-1}L(\hat y,y) \] 其中，N为本次参加训练的样本个数。

我们进行梯度下降时使用的是代价函数求偏导，而对代价函数求偏导其实只需要对损失函数求偏导，然后求个平均就是代价函数求偏导。所以接下来的求偏导过程写的是对损失函数求偏导。不过在最后的总结时，会对损失函数求偏导的结果求平均变成代价函数求偏导的结果。

softmax的损失函数表达式

softmax分类器选用的是交叉熵损失函数。有的文章也说是选用对数损失函数。这是因为：

对数损失函数(Log loss function)和交叉熵损失函数(Cross-entroy loss function)表达式本质式一样的。不过这两种损失函数对应的上一层结构不同，对数损失函数经常对应的是Sigmoid函数的输出，用于二分类问题；而交叉熵损失函数经常对应的是Softmax函数的输出，用于多分类问题。详情请见相关文章【3】。

\[ L(\hat y,y) = -\sum_{k=1}^Ky_kloga_k \]

注，log通常以2为底，有的文章也会使用ln。

其中：

$\hat y$: 单个训练样本label预测值，$y = (a_1,...,a_k) $; 例如：$y = (0.055,0.090,0.0067,0.10,0.74,010)$
$y$:单个训练样本label真实值,$y = (y_1,...,y_k)$; 例如：$y = (0,0,0,0,1,0)$
$y_k$: 单个训练样本属于第k类的真实值，取值0或1
$a_k$：单个训练样本属于第k类的预测值，为一个概率值

对代价函数进行梯度下降

梯度下降算法步骤

回顾梯度下降算法的步骤：

初始化模型未知参数$W = (w_1,..,w_K)$，其中每一个$w_k$ 为向量，维度与样本x相同。K的值与类别数相同。
重复进行以下公式直到收敛：

\[ w_k = w_k - a\frac{\partial J}{\partial w_k},\quad k = 0,1,...,K-1 \]

对上述公式进行说明：

为什么没有$b_k$?

$b_k$被融合到向量$w_k$里了。最后总结结果时会单独把$b_k$ 提出来。

$a$是什么？

学习率，是需要人工调整的超参数。它控制的是梯度下降中每一步的跨度大小。关于学习率更多说明请见相关文章【1】。

这个公式里明明是对代价函数J求偏导，为什么下面推导的是损失函数求偏导？

刚才在区分代价函数和损失函数时有说过，对求得的损失函数偏导求平均就是代价函数求偏导的结果。

损失函数求偏导的详细推导

此部分参考了文章：参考文章【1】

之前提到的softmax损失函数： \[ L(\hat y,y) = -\sum_{k=1}^Ky_kloga_k~~~~~(1) \] 其中， \[ \begin{split} & a_k = \frac{e^{z_k}}{\sum_{i=1}^Ke^{z_i}}~~~~~~(2) \\ & z_k = w_k^Tx = \sum_{i=1}^Mw_{k,i}x_i~~~(3)\\ & k = 0,1,...,K-1 \end{split} \] 现在需要求：$\frac{\partial L(\hat y,y)}{\partial w_k}$

根据链式求导法则,有： \[ \frac{\partial L(\hat y,y)}{\partial w_k} = \frac{\partial L(\hat y,y)}{\partial z_k}·\frac{\partial z_k}{\partial w_k}~~~~(4) \]

1 求解$\frac{\partial z_k}{\partial w_k}$ \[ \begin{split} \frac{\partial z_k}{\partial w_k} & = \frac{\partial (w_k^Tx)}{\partial w_k} = x ~~~~(5) \end{split} \]

2 求解$\frac{\partial L(\hat y,y)}{\partial z_k}$

这也是整个softmax最关键的一步，很多教程推完这里就结束了。

根据（2）式，$a_j$ 均包含$z$的所有分量,所以要求$z_k$ 的偏导，所以对于$z_k$的偏导，每一个$a_j$ 都有贡献： \[ \frac{\partial L(\hat y,y)}{\partial z_k} = \sum_{j=1}^K[\frac{\partial L(\hat y,y)}{\partial a_j}\frac{\partial a_j}{\partial z_k}]~~~~(6) \] 2.1 求解$\frac{\partial L(\hat y,y)}{\partial a_j}$ \[ \begin{split} \frac{\partial L(\hat y,y)}{\partial a_j} & = \frac{\partial (-\sum_{j=1}^Ky_jloga_j)}{\partial a_j} = - \frac{y_j}{a_j}~~~~(7) \end{split} \]

2.2 求解$\frac{\partial a_j}{\partial z_k}$

刚才说过，每一个$a_j$ 都要对$z_k$ 求导，那自然有两种情况：$j = k$ 和$j \neq k$ 。现在对这两种情况分开讨论。

2.2.1 当$j \neq k$ \[ \begin{split} \frac{\partial a_j}{\partial z_k} &= \frac{\partial(\frac{e^{z_j}}{\sum_{i=1}^Ke^{z_i}})}{\partial z_k} \\ & = -e^{z_j}\frac{1}{(\sum_{i=1}^Ke^{z_i})^2}e^{z_k} \\ & = -\frac{e^{z_j}}{\sum_{i=1}^Ke^{z_i}}·\frac{e^{z_k}}{\sum_{i=1}^Ke^{z_i}} \\ & = -a_ja_k ~~~~~(8) \end{split} \] 2.2.2 当$j=k$ $$ \[\begin{split} \frac{\partial a_j}{\partial z_k} &= \frac{\partial a_k}{\partial z_k}\\ &=\frac{\partial(\frac{e^{z_k}}{\sum_{i=1}^Ke^{z_i}})}{\partial z_k} \\ & = \frac{e^{z_k}\sum_{i=1}^Ke^{z_i}-(e^{z_k})^2}{(\sum_{i=1}^Ke^{z_i})^2} \\ & = \frac{e^{z_k}}{\sum_{i=1}^Ke^{z_i}}(1-\frac{e^{z_k}}{\sum_{i=1}^Ke^{z_i}}) \\ & = a_k(1-a_k)~~~~(9) \end{split}\] \[ **2.2.3 将（7）、（8）、（9）代入（6）求解** \] \[\begin{split} \frac{\partial L(\hat y,y)}{\partial z_k} & = \sum_{j=1}^K[\frac{\partial L(\hat y,y)}{\partial a_j}\frac{\partial a_j}{\partial z_k}] \\ & = \sum_{j=1}^K[-\frac{y_j}{a_j}\frac{\partial a_j}{\partial z_k}] \\ & = -\frac{y_k}{a_k}\frac{\partial a_k}{\partial z_k}+\sum_{j=1,j\neq k}^K[-\frac{y_j}{a_j}\frac{\partial a_j}{\partial z_k}] \\ & = -\frac{y_k}{a_k}a_k(1-a_k)+\sum_{j=1,j\neq k}^K[-\frac{y_j}{a_j}·-a_ja_k] \\ & = y_k(a_k-1)+\sum_{j=1,j\neq k}^Ky_ja_k \\ & = -y_k+y_ka_k+\sum_{j=1,j\neq k}^Ky_ja_k \\ & = -y_k+a_k\sum_{j=1}^Ky_j~~~~(10) \end{split}\]

$$ ok,到这里已经初步求出了损失函数对$z_k$ 的偏导。不过我们还可以对它进一步优化，所以我们现在考虑y的特点，前面说过：

$y$:单个训练样本label真实值,$y = (y_1,...,y_k)$; 例如：$y = (0,0,0,0,1,0)$

也就是说向量y中只有一个值为1,所以$\sum_{j=1}^Ky_j = 1$ 。

于是(9)式将变为: \[ \frac{\partial L(\hat y,y)}{\partial z_k} = a_k-y_k~~~~(11) \] 其中，

$a_k$: 单个训练样本属于第k类的预测值，为一个概率值。
$y_k$: 单个训练样本属于第k类的真实值，取值0或1

到此为止，softmax最核心的偏导已经推导完毕。多么简约美妙的一个公式！

3.将（5）、（11）代入（4）求解L对$w_k$的偏导 \[ \begin{split} \frac{\partial L(\hat y,y)}{\partial w_k}& = \frac{\partial L(\hat y,y)}{\partial z_k}·\frac{\partial z_k}{\partial w_k} \\ & = (a_k-y_k)x \end{split} \] 3.1 取出$b_k$

最开始说了，我们计算时先把$b_k$ 融进$w_k$ 了。现在将它取出来：

因为把$b_k$融合进$w_k$ 后，$w_k$最后一个分量为$b_k$ 。而$x$最后一个分量为1。所以 $z_k$对$w_k$ 求偏导后，$b_k$那个分量对应的偏导就是1。所以 \[ \frac{\partial L(\hat y,y)}{\partial b_k} =a_k-y_k \]

结果总结

好了，现在来总结一下softmax损失函数求偏导的结果： \[ \begin{split} & \frac{\partial L(\hat y,y)}{\partial w_k} = (a_k-y_k)x \\ & \frac{\partial L(\hat y,y)}{\partial b_k} =a_k-y_k \end{split} \]

更新权重

还记得梯度下降的步骤吗？

梯度下降更新权重时，是用的代价函数的偏导更新的，我们刚才求导的只是损失函数的偏导。所以还需要对它们求平均。 \[ \begin{split} & \frac{\partial J}{\partial w_k} = \frac{1}{N}\sum_{i=0}^{N-1}(a_k-y_k)x \\ & \frac{\partial J}{\partial b_k} = \frac{1}{N}\sum_{i=0}^{N-1}(a_k-y_k) \end{split} \] 其中，N为本次参加训练的样本个数。另外，上述式子省去了上标$i$，上标$i$表示这是第i个样本。

顺带一提，像上面这种根据推出的结果反过去更新权重的流程，在神经网络中被称为反向传播。

总结

softmax多分类模型的训练流程

给定训练集X，训练集X共分为K类:

随机初始化模型未知参数$\theta$ ，本篇文章中为随机初始化权重向量$w_k,b_k,k=1,2,...,K-1$。其中，$w_k$为向量，$b_k$ 为标量。
梯度下降算法迭代更新模型参数直至收敛，每一轮具体流程如下：
1. 先通过正向传播求得本轮训练样本预测值。
2. 反向传播更新模型参数：
\[ \begin{split} & w_k = w_k - a\frac{\partial J}{\partial w_k} = w_k-a\frac{1}{N}\sum_{i=0}^{N-1}(a_k-y_k)x,\quad k = 0,1,...,K-1 \\ & b_k = b_k -a\frac{\partial J}{\partial b_k} = b_k-a\frac{1}{N}\sum_{i=0}^{N-1}(a_k-y_k),\quad k = 0,1,...,K-1 \end{split} \]
注意：上述公式省去了上标i，上标i表示这是第i个样本。

softmax多分类模型的预测流程

经过训练后，模型参数已经确定。现在只需要用这些参数对需要预测的数据跑一遍正向传播就行。

不过可能在求出预测值后，需要加一步判断：哪个类别的概率最大，就认为该样本属于哪一类。

到此，整个softmax分类器说明完毕。

softmax多分类器的具体代码实现和应用

关于softmax的具体代码实现和应用将在下一篇文章介绍。在下一篇文章中，将会以经典的鸢尾花数据集为例，对其进行softmax多分类的手动代码实现。

下篇文章：机器学习笔记14——【Softmax多分类 2】代码具体实现与应用（含数据集） | issey的博客

机器学习笔记13——【Softmax多分类 1】完整流程与详细公式推导

推荐阅读

前言