前言

本文是现阶段图像变换笔记的最后一篇，将介绍图像的正交变换。

图像正交变换简介

正交变换是数字图像处理的一种有效工具。通过正交变换，我们可以将图像从时域变换到频域进行后续处理。正交变换在图像增强、图像复原、图像压缩、图像特征处理等方面都经常使用。

常用的正交变换有:离散傅里叶变换、离散余弦变换、K-L变换、小波变换等。本篇仅介绍傅里叶变换和离散余弦变换的相关内容，K-L变换和小波变换将会在后续文章补齐（希望吧）。

离散傅里叶变换

图像处理中的离散傅里叶变换其实指的是二维快速离散傅里叶变换。关于傅里叶原理与推导在之前的文章已经详细写过，详情请见"相关文章"。这里默认已经对傅里叶变换/二维离散傅里叶变换有一定了解。

对图像进行离散傅里叶变换的作用

可以将空间域（二维灰度数表）的图像转换到频域（频率数表），使得可以更方便的处理图像，也更有利于进行频域滤波等操作。

二维离散傅里叶变换

公式： \[ \begin{split} & F(u,v) = \sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-i2\pi(\frac{ux}{M}+\frac{vy}{N})} \\ & f(u,v) = \frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}F(x,y)e^{i2\pi(\frac{ux}{M}+\frac{vy}{N})} \end{split} \] 不过实际上要使用二维离散傅里叶变换，是使用的对其进行分治的基础上得到的快速二维傅里叶变换。

频谱图

学习图像离散傅里叶变换，一个不得不提的就是对频谱图的理解。光有公式是不够的，还得看懂变换后的频谱图大概代表什么意思。频谱图的内容较多，我在学习时找到了很详细的文章。请见参考教程【1】。推荐先去看频谱图，这里虽然占的篇幅很少，实际上是因为自己太懒了不想重述了。

二维频谱图中每一点都是一个与之一一对应的二维正弦/余弦波。

示例

matlab中使用fft2进行二维（快速）离散傅里叶变换。

使用文档：二维快速傅里叶变换 - MATLAB fft2 - MathWorks 中国

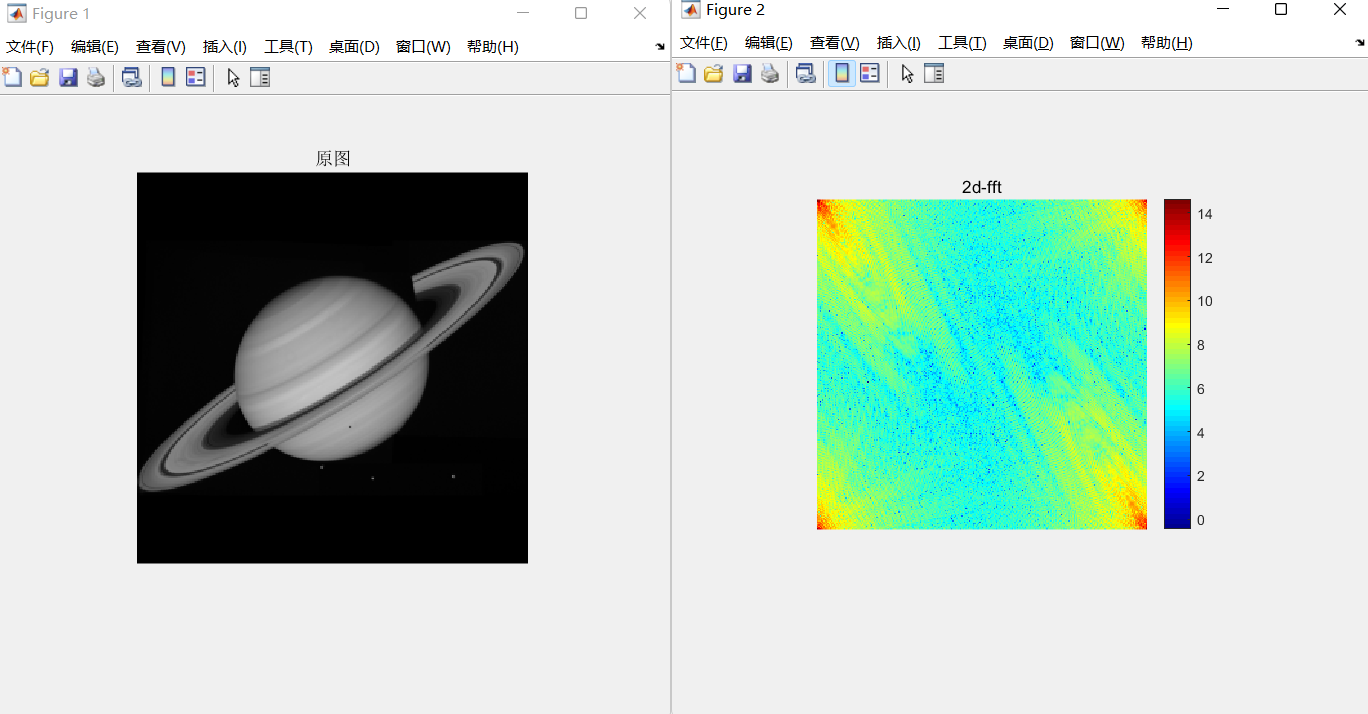
将时域图转化为频域图:

clc;clear;close all; 
load imdemos saturn2;
figure,imshow(saturn2);
title('原图');
X = fft2(saturn2);
figure,imshow(log(abs(X)),[]);
title('2d-fft');
colormap(jet(64)),colorbar;

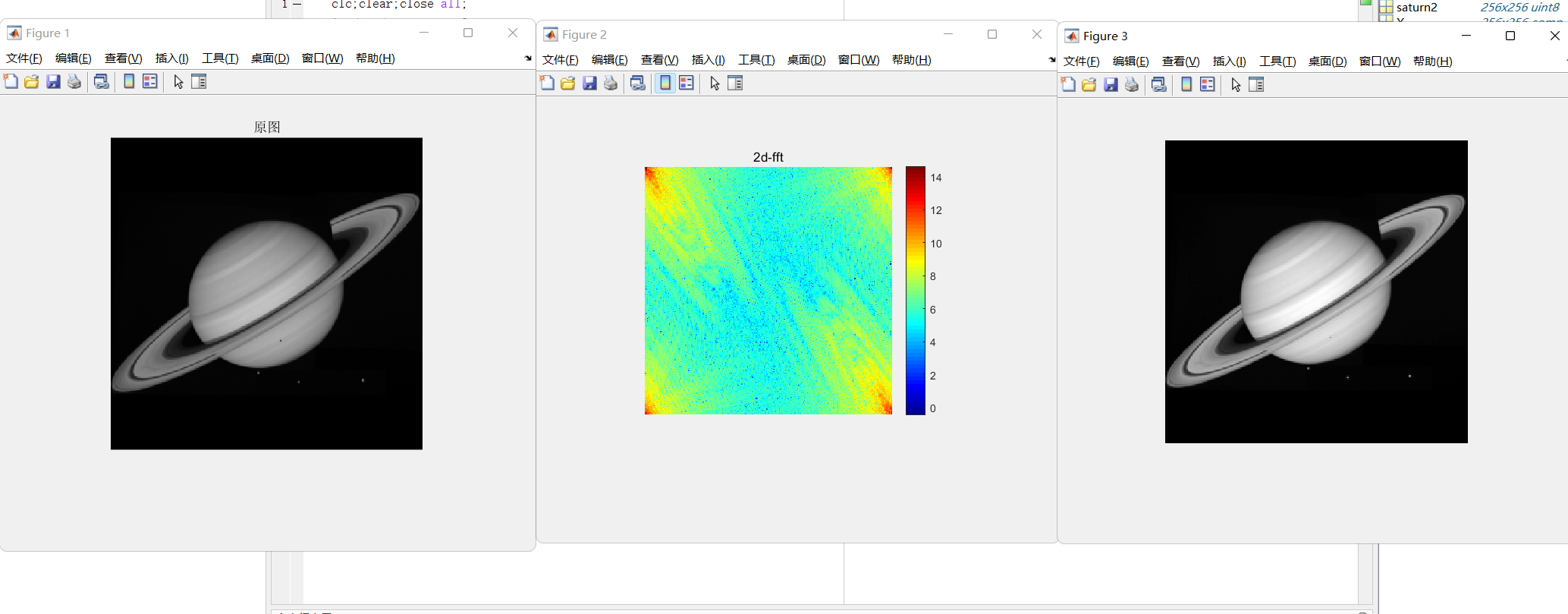
在频域去阈值后再逆变换

clc;clear;close all; 
load imdemos saturn2;
figure,imshow(saturn2);
title('原图');
X = fft2(saturn2);
figure,imshow(log(abs(X)),[]);
title('2d-fft');
colormap(jet(64)),colorbar;
X(abs(X)<10)=0;
Y = real(ifft2(X)/255);
figure(),imshow(Y,[]);

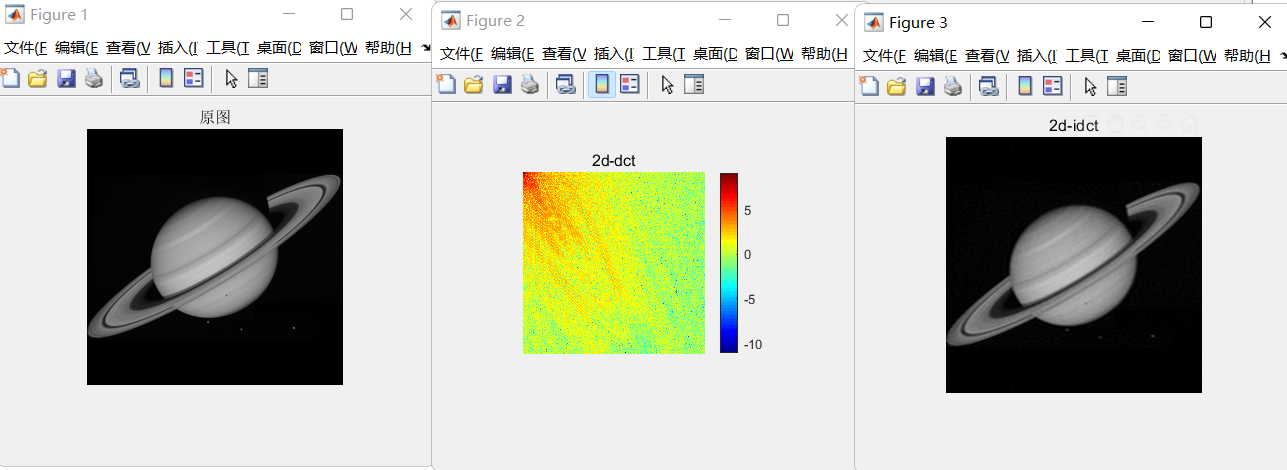
离散余弦变换

简介

离散余弦变换(Discrete Cosine Transform, DCT)是以一组不同频率和幅值的余弦函数和来近似一幅图像，实际上是傅立叶变换的实数部分。离散余弦变换有一个重要的性质，即对于一幅图像，其大部分可视化信息都集中在少数的变换系数上。因此，离散余弦变换经常用于图像压缩，例如国际压缩标准的JPEG格式中就采用了离散余弦变换。

基本原理

在傅立叶变换过程中，若被展开的函数是实偶函数，则其傅立叶变换中只包含余弦项，基于傅立叶变换的这一特点，人们提出了离散余弦变换。DCT变换先将图像函数变换成偶函数形式，再对其进行二维离散傅立叶变换，故DCT变换可以看成是一种简化的傅立叶变换。

二维离散余弦公式：

对于\((M,N)\) 的序列矩阵\(f(x,y)\)，二维离散余弦变换定义如下：

DCT: \[ F(u,v) = a(u)a(v)\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)cos\frac{(2x+1)u\pi}{2M}cos\frac{(2y+1)u\pi}{2N} \] 其中,\(u=0,1,...,M-1,v=0,1,...,N-1\) \[ a(u) =\left\{ \begin{aligned} \frac{1}{\sqrt M},u=0\\ \sqrt \frac{2}{M},u\neq0\\ \end{aligned} \right.,a(v) =\left\{ \begin{aligned} \frac{1}{\sqrt N},v=0\\ \sqrt \frac{2}{N},v\neq0\\ \end{aligned} \right. \] IDCT: \[ f(x,y) = \sum_{x=0}^{M-1}\sum_{y=0}^{N-1}a(u)a(v)F(u,v)cos\frac{(2x+1)u\pi}{2M}cos\frac{(2y+1)u\pi}{2N} \] 其中,\(x=0,1,...,M-1,y=0,1,...,N-1\) \[ a(u) =\left\{ \begin{aligned} \frac{1}{\sqrt M},u=0\\ \sqrt \frac{2}{M},u\neq0\\ \end{aligned} \right.,a(v) =\left\{ \begin{aligned} \frac{1}{\sqrt N},v=0\\ \sqrt \frac{2}{N},v\neq0\\ \end{aligned} \right. \]

示例

matlab中使用dct2进行二维离散余弦变换。

参考文档：二维离散余弦变换 - MATLAB dct2 - MathWorks 中国

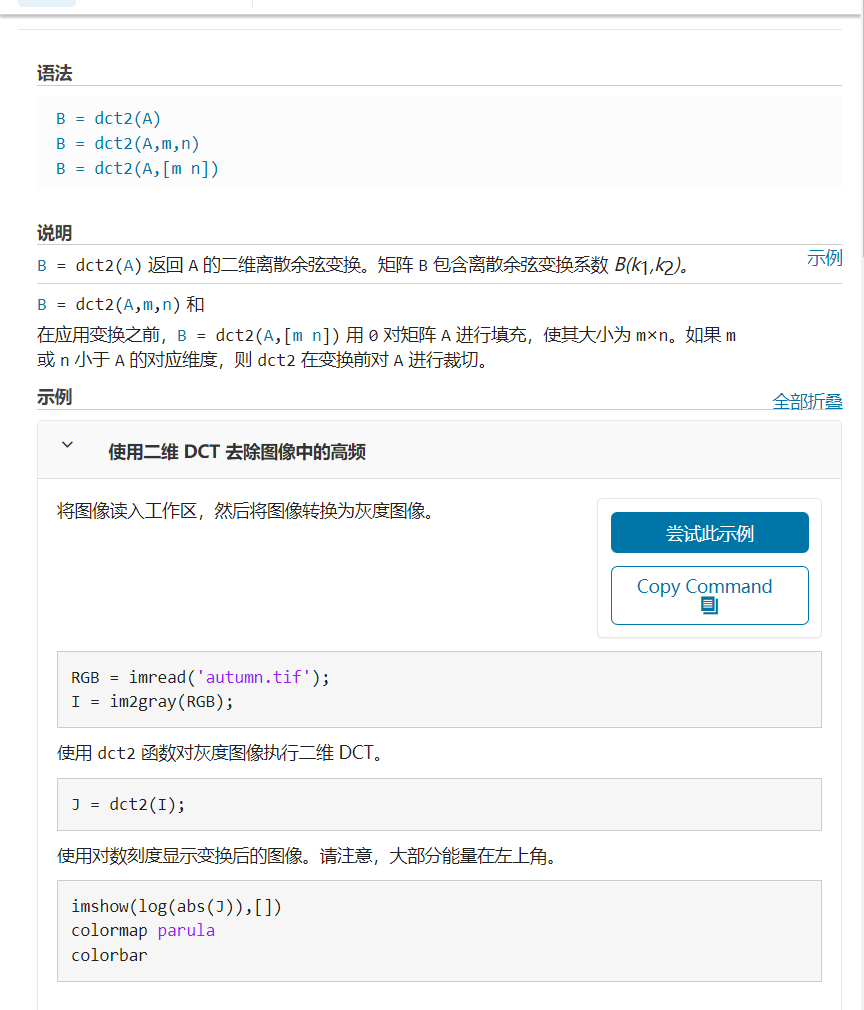
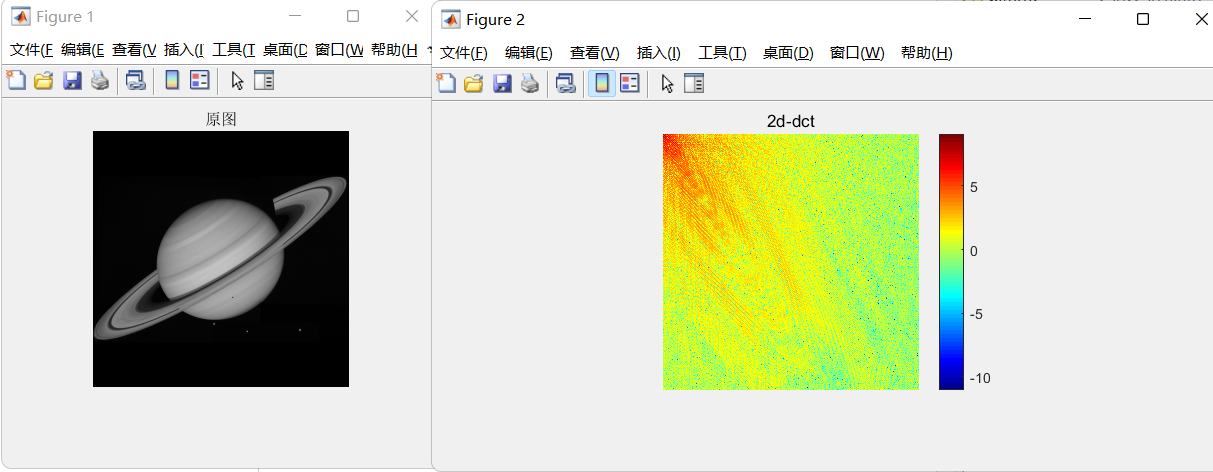
正变换：

clc;clear;close all; 
load imdemos saturn2;
figure,imshow(saturn2);
title('原图');
X = dct2(saturn2);
figure,imshow(log(abs(X)),[]);
title('2d-dct');
colormap(jet(64)),colorbar;

在频域设置阈值并逆变换：

clc;clear;close all; 
load imdemos saturn2;
figure,imshow(saturn2);
title('原图');
X = dct2(saturn2);
figure,imshow(log(abs(X)),[]);
title('2d-dct');
colormap(jet(64)),colorbar;
X(abs(X)<10)=0;
Y = idct2(X)/255;
figure(),imshow(Y);
title('2d-idct');

【matlab图像处理笔记5】【图像变换】（四）图像的正交变换

推荐阅读

前言