前言：请确保你已学会了前几个线性回归的内容。之前涉及的相关概念在此文章不会再提及。

什么是逻辑回归？

逻辑回归是一种广义的线性回归模型，主要用于解决二分类问题。所谓二分类问题，就是比如判断一个邮件是否是垃圾邮件、根据某些特征判断肿瘤是否为恶性肿瘤等问题，我们可以将是/否表示为1/0。简单的二分类数据图如下：

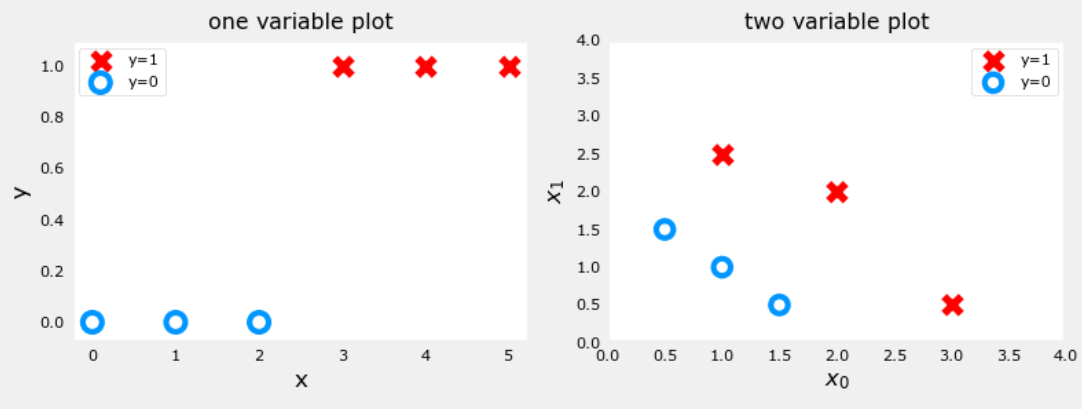
（注：左图为只有一个特征的数据模拟图，右图为有两个特征的数据模拟图。）

以仅有一个特征的二分类（左图）为例，如果我们模拟传统线性回归\(f(x) = \vec w\cdot \vec x+b\)，并选择0.5作为阈值：当\(y \geq 0.5\)时我们认为它是种类1，当\(y<0.5\)时，我们认为它是种类0，那么可以得到以下图像：

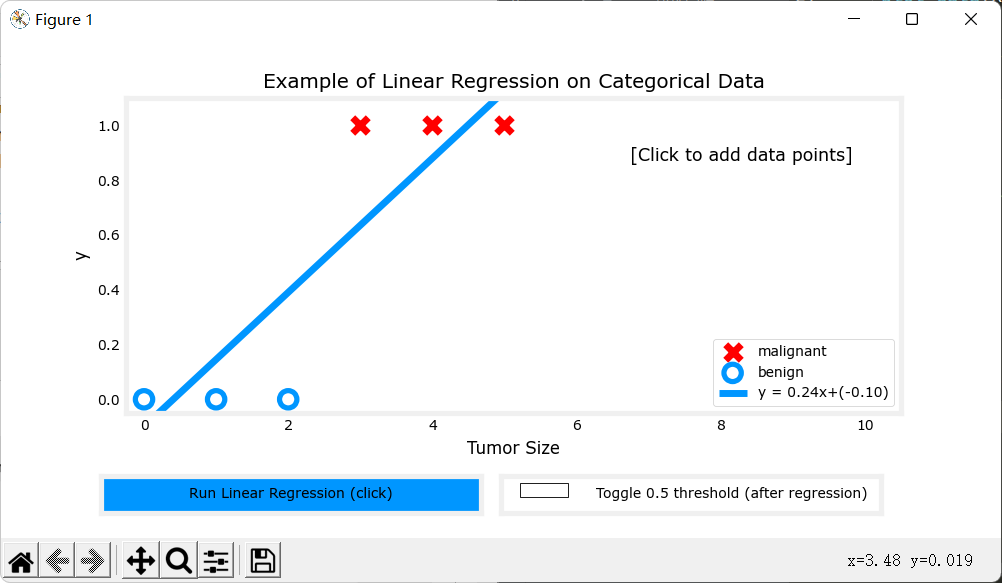
但是，当我们再加一些数据，它就会模拟成这样：

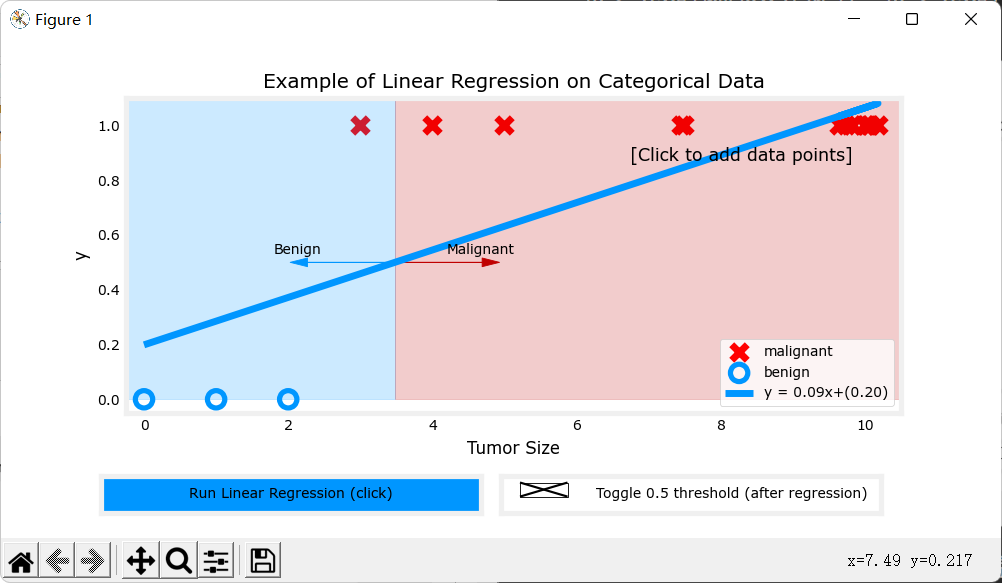
很明显能看出，这样的预测并不准确。

所以当对二分类问题进行回归分析时，采用传统的线性回归函数进行拟合并不是一个好的方案。于是我们将使用另一种函数——Sigmoid函数。

Sigmoid函数

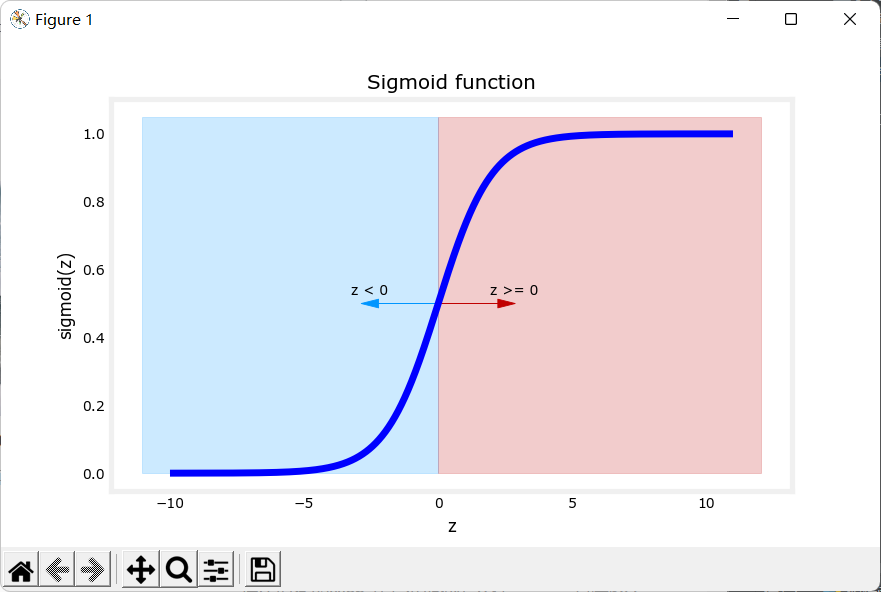
Sigmoid函数又称为Logistic函数（逻辑函数），Sigmoid函数输出值在\((0,1)\)之间，而且可以解决离群点对拟合线性回归的影响，Sigmoid函数在诸多领域都有涉及，这里不再拓展。

Sigmoid函数表达式：\(g(z) = \frac{1}{1+e^{-z}}\)

函数图像：

现在使用sigmoid函数拟合上面的例子，当\(g(z)\geq 0.5\)时，我们认为它属于种类1，当\(g(z)<0.5\)时，我们认为它属于种类0,于是可以得到下面的图像：

（注：橙色的线为决策边界，后面会详细解释。）

很明显看出该函数拟合的很好。

决策边界

上面提到，我们使用sigmoid函数进行预测时，当\(g(z) \geq 0.5\)，我们认为是种类1，当\(g(z)<0.5\)时，我们认为是种类0。那么，什么时候\(g(z)\)等于0.5呢？观察sigmoid函数的图像，当\(z\)等于0时，\(g(z) = 0.5\)。所以我们令\(z = f_{\vec w,b}(\vec x) = \vec w\cdot\vec x+b\),决策边界即\(f_{\vec w,b}(\vec x) = 0\)。

以上述右图为例（即以有两个特征的二分类为例），决策边界最终求出的函数为\(f(x) = x_0+x_1 -3\)。当\(f(x) \geq 0\)，属于种类1；当\(f(x)<0\)，属于种类0。图像为：

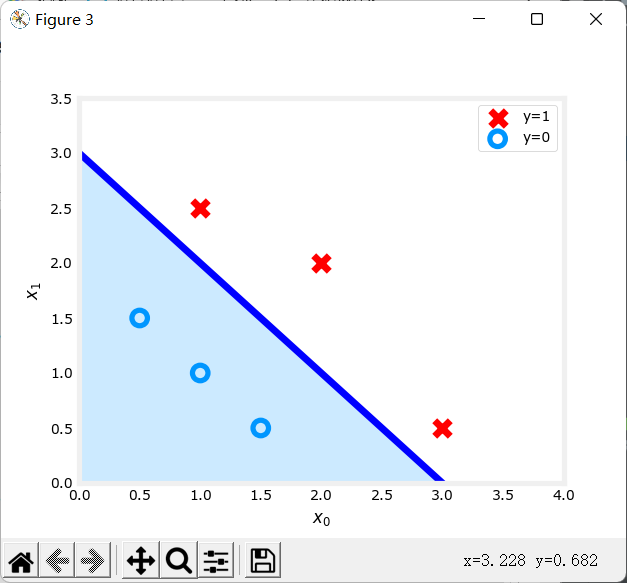
可以看到决策边界将两个不同的种类分开了。

又比如，当\(f_{\vec w,b}(\vec x)\)为更复杂的多项式时，可以画出以下图像：

逻辑回归的损失函数

为什么平方误差模型不可行？

在之前的线性回归中，我们使用平方误差作为我们的代价函数（损失函数）：、

\[ \begin{split}J(\vec{w},b) = \frac {1} {2m}\sum_{i = 0}^{m-1}(\hat y^{(i)}-y^{(i)})^2 \\=\frac {1} {2m}\sum_{i = 0}^{m-1}(f_{\vec w,b}(\vec x^{(i)})-y^{(i)})^2\end{split} \]

其中，\((i)\)为样例序号。

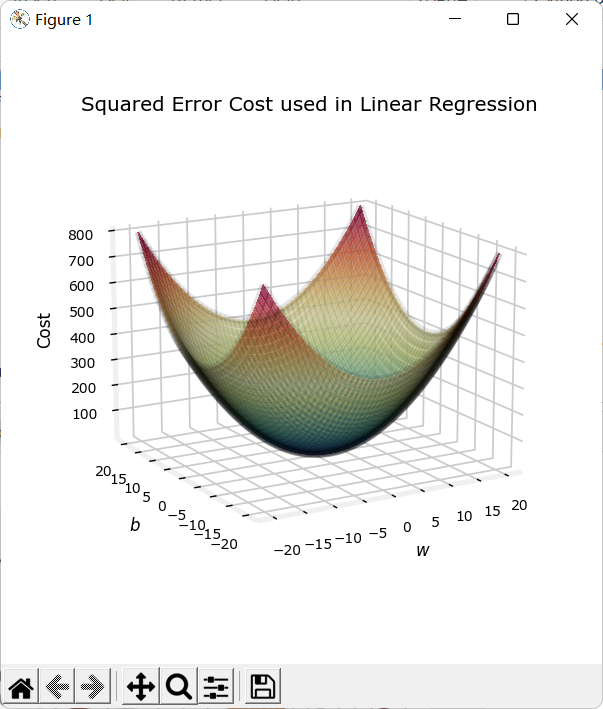
那时\(f_{\vec w,b}(\vec x) = \vec w\cdot\vec x+b\),平方误差代价函数可以平滑下降直到一个最低点。

下图是一元一次线性回归\(f(x) = wx+b\)的代价函数图像：

但是逻辑回归的函数为\(sigmoid(\vec w\cdot\vec x+b) = \frac{1}{1+e^{-z}}\)，其中，\(z = \vec w\cdot\vec x+b\)。

如果再使用平方误差作为代价函数，它的图像将会是凹凸不平的：

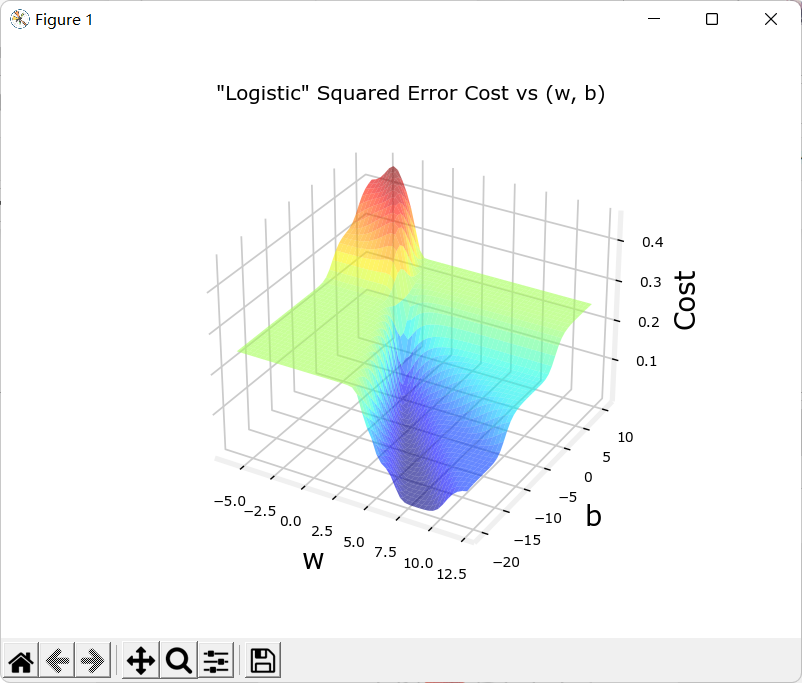
这意味着梯度下降算法很可能无法找到最低点，会卡在某个极小值点。

为了解决这个问题，我们将使用另一种模型作为我们的代价函数：

对数损失函数

为什么使用对数损失函数作为逻辑回归的损失函数而不使用其他函数？

使用对数损失函数作为逻辑回归的损失函数是由极大似然估计推导所得，这里不进行拓展。

单个样例损失：

\[ L(\hat y,y) = \left\{ \begin{aligned} -log(\hat y) if\quad y = 1\\ -log(1-\hat y) if\quad y = 0\\ \end{aligned} \right. \]

其中，\(\hat y = g_{\vec w,b}(\vec x) = sigmoid(\vec w\cdot \vec x+b)，\hat y\in (0,1)\)

解释一下含义：

当真实值为1时，图像为：

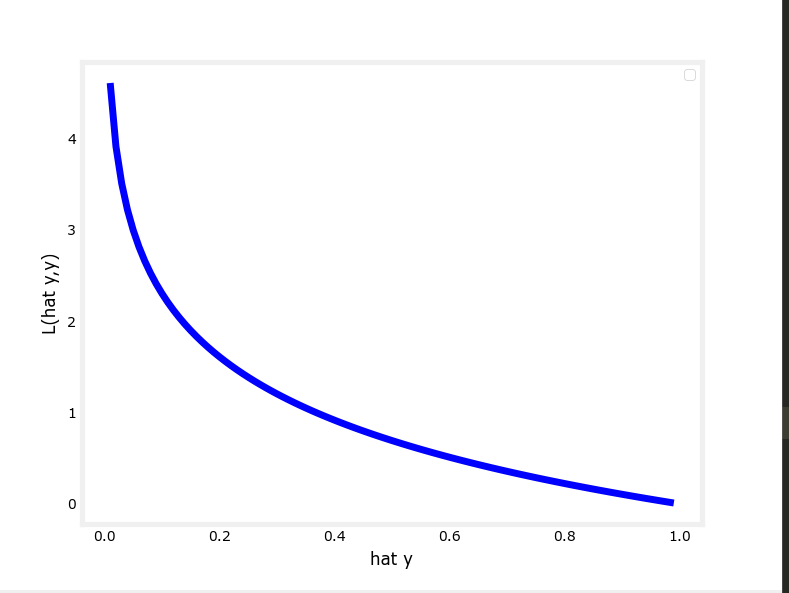
可以看出，在真实值y为1的情况下：当预测值\(\hat y\)接近1时，计算出的损失很小；而当\(\hat y\)接近0时，计算出的损失很大很大。换成人话，就是比如说某人真实情况是“很胖”，但是预测出的却是“很廋”，这时预测值和真实值的差距就很大很大。

同理，当真实值为0时，图像为：

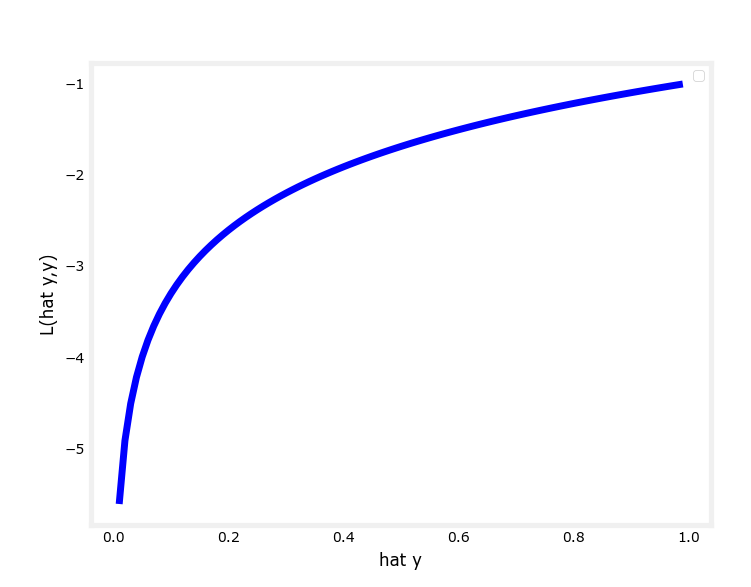
在真实值y为0的情况下：当预测值\(\hat y\)接近0时，计算出的损失很小；而当\(\hat y\)接近0时，计算出的损失很大很大。

化简\(L(\hat y,y)\),可得\(L(\hat y,y) = -ylog(\hat y)-(1-y)log(1-\hat y)\)

逻辑回归损失函数

上式求和即可得：

公式：\(J(\vec w,b) = \frac 1 m \sum_{i=0}^{m-1}L(g_{\vec w,b}(\vec x),y)\)

让我们用这个新的代价函数模拟一下最开始左图的代价函数模型：

现在这个图像很适合使用梯度下降算法来找到它的最低点。

梯度下降算法

步骤与线性回归相同，同时进行以下直到收敛：

\(w_j = w_j - a\frac{\partial J(\vec w,b)}{\partial w_j},\quad j = 0,1,...,n-1\)

\(b = b - a\frac{\partial J(\vec w,b)}{\partial b}\)

其中，

\(\frac{\partial J(\vec w,b)}{\partial w_j} = \frac{1}{m}\sum_{i=0}^{m-1}(g_{\vec w,b}(\vec x^{(i)})-y^{(i)})x_j^{(i)}\)

\(\frac{\partial J(\vec w,b)}{\partial b} = \frac{1}{m}\sum_{i=0}^{m-1}(g_{\vec w,b}(\vec x^{(i)})-y^{(i)})\)

这两个偏导求出来的公式和线性回归的几乎长得一样，但是并不代表他们一样。

这里\(g_{\vec w,b}(x) = sigmoid(\vec w\cdot \vec x+b)\)

求导过程请参考文章：逻辑回归梯度下降法

现在只需要利用该算法求得\(\vec w,b\)即可。

关于多分类问题：多分类问题也可以使用逻辑回归解决。之后会出专门的文章，这里暂时不写。

补充：F1-score评价指标

F1-Score简介

F1分数（F1 Score），是统计学中用来衡量二分类模型精确度的一种指标。它同时兼顾了分类模型的精确率和召回率。F1分数可以看作是模型精确率和召回率的一种加权平均，它的最大值是1，最小值是0。

相关概念

下面先介绍几个概念：

  • TP（rue Positive）：正样本被判定为正样本

  • FP（False Positive）：负样本被判定为正样本

  • TN（True Negative）：负样本被判定为负样本

  • FN（False Negative）：正样本被判定为负样本

精确度/查准率：指分类器预测为正例中正样本所占比重：

\(Precision = \frac {TP} {TP+FP}\)

召回率/查全率：指预测为正例占总正例比重：

\(Recall = \frac {TP}{TP+FN}\)

F-Score算法将同时使用以上两个公式，此外，介绍另一种常用的准确率概念：

准确率，指分类器判断正确的占总样本的比重：

\(Accuracy = \frac {TP+TN}{TP+TN+FP+FN}\)

F-Score

具体来源等等就不拓展了，有兴趣可以自查。

F-Score是可以综合考虑精确度（Precision）和召回率（Recall）的调和值，公式如下：

\(F Score = (1+\beta^2)*\frac{Precision*Recall}{\beta^2Precision+Recall}\)

当\(\beta=1\)时，被称为F1-Score或F1-Measure。此时精确度和召回率权重相同。

当我们认为精确度更重要，调整\(\beta\)<1；

当我们认为召回率更重要，调整\(\beta\)>1。

示例及代码：

数据来源：

https://www.kaggle.com/datasets/muratkokludataset/pumpkin-seeds-dataset

问题描述：

现在有两类南瓜种子（CERCEVELIK, URGUP_SIVRISI）以及它们的一些特征：

1
2
3
4
5
6
7
8
9
10
11
12
@ATTRIBUTE Area    INTEGER
@ATTRIBUTE Perimeter    REAL
@ATTRIBUTE Major_Axis_Length    REAL
@ATTRIBUTE Minor_Axis_Length    REAL
@ATTRIBUTE Convex_Area    INTEGER
@ATTRIBUTE Equiv_Diameter    REAL
@ATTRIBUTE Eccentricity    REAL
@ATTRIBUTE Solidity    REAL
@ATTRIBUTE Extent    REAL
@ATTRIBUTE Roundness    REAL
@ATTRIBUTE Aspect_Ration    REAL
@ATTRIBUTE Compactness    REAL

现在请根据已知数据集对这两类南瓜种子进行（逻辑回归）分类并判断准确率。

代码说明：会使用sklearn进行数据分割以及模型评价（F1-score），逻辑回归部分全部自主实现。

所需要的包

1
2
3
4
5
import pandas as pd
import numpy as np
import math,copy
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

数据预处理

特征选择与数据集拆分

为了可视化，这里只选择其中两个特征作为特征集（Major_Axis_Length、Minor_Axis_Length）。

导入和提取数据、拆分训练集和数据集：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 导入数据
data = pd.read_excel(r'.\Pumpkin_Seeds_Dataset\Pumpkin_Seeds_Dataset.xlsx',0)
df = pd.DataFrame(data)

# 转换数据
color = []
label = []
for i in df['Class']:
    if i == 'Çerçevelik':
        label.append(0)
    elif i == 'Ürgüp Sivrisi':
        label.append(1)

# 提取所需数据
x_1 = np.array(df['Major_Axis_Length']).reshape(-1,1)
x_2 = np.array(df['Minor_Axis_Length']).reshape(-1, 1)
X_features = np.c_[x_1,x_2]
Y_target = np.array(label)

# 拆分训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(X_features,Y_target,train_size=0.5,random_state=45)

特征缩放（Z-score标准化）

注意：特征缩放一定要用对地方，应该在拆分完训练集和测试集后，仅对训练集使用，不应该把训练集和测试集放在一起标准化，对测试集的操作应该是在对训练集标准化后，使用通过训练集标准化时计算得到的平均值、方差等进行标准化。

这里使用Z-score标准化进行特征缩放。

1
2
3
4
5
6
7
8
9
10
# Z-score标准化
def Zscore(X):
    '''x是(m,n)的矩阵，m为样本个数，n为特征数目'''
    # 找每列(特征)均值
    mu = np.mean(X,axis=0)
    # 找每列(特征)标准差
    sigma = np.std(X,axis=0)
    X_norm = (X - mu) / sigma

    return X_norm,mu,sigma
1
2
3
4
5
6
7
8
9
10
11
12
# 标准化特征集
X_train,mu,sigma = Zscore(X_train)
# 绘制训练集
for i in y_train:
     if i == 1:
         color.append("blue")
     else:
         color.append("orange")
plt.scatter(X_train[:,0],X_train[:,1],color = color)
plt.xlabel('Major_Axis_Length')
plt.ylabel('Minor_Axis_Length')
plt.show()

标准化后的训练集：

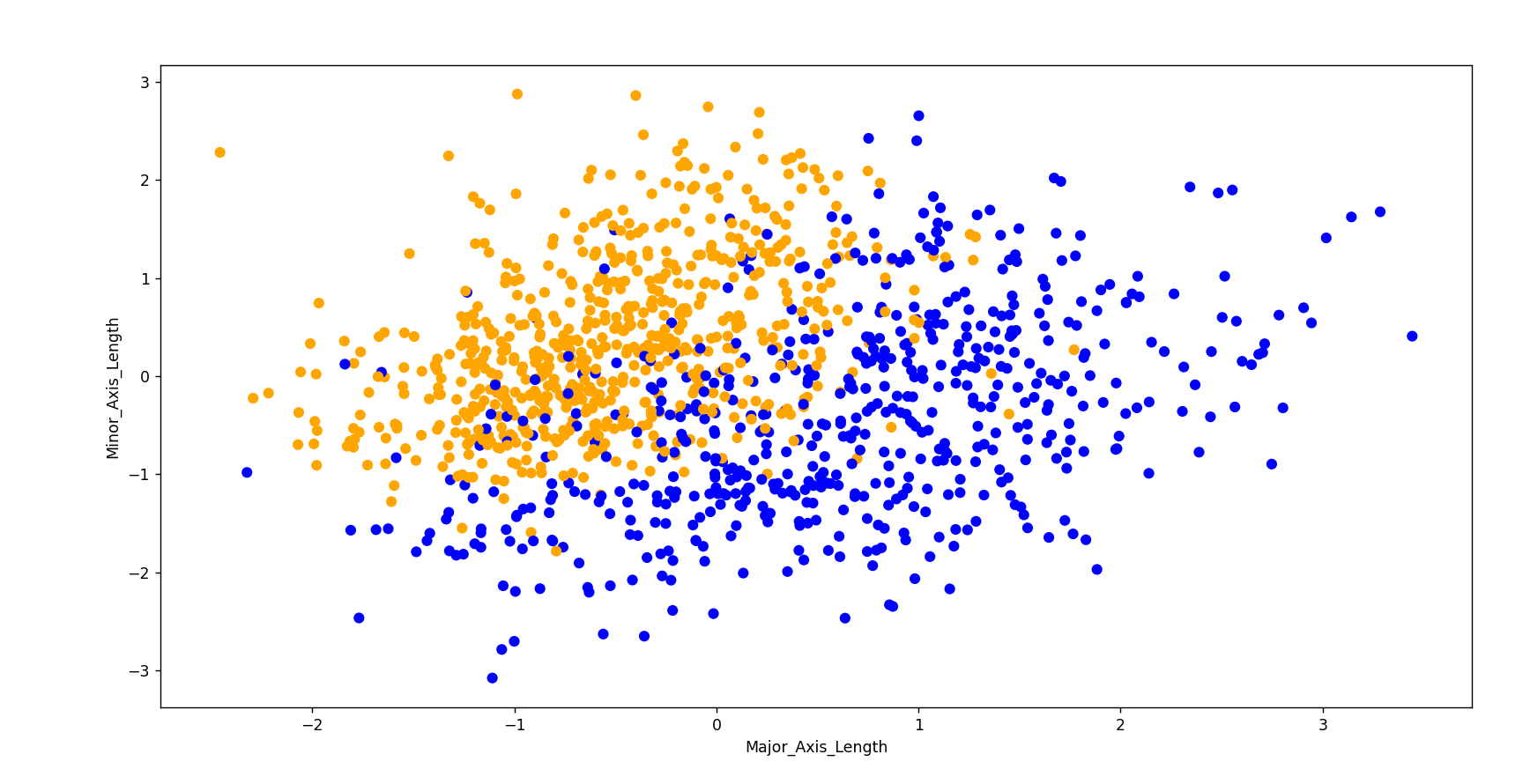
注：橘色为Çerçevelik种类，蓝色为Ürgüp Sivrisi种类。

实现逻辑回归

sigmoid函数

公式：\(g(z) = \frac{1}{1+e^{-z}}\)

1
2
3
4
5
6
7
8
def sigmoid(z):
    '''

    :param z: 标量
    :return: 标量
    '''
    g = 1 / (1 + np.exp(-z))
    return g

损失函数

公式：\(J(\vec w,b) = \frac 1 m \sum_{i=0}^{m-1}L(g_{\vec w,b}(\vec x),y)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 逻辑回归损失函数
def compute_cost_logistic(X, y, w, b):
    '''

    :param X: 特征集，矩阵
    :param y: 目标值，列表
    :param w: 向量
    :param b: 标量
    :return: 对数损失值，标量
    '''

    m = X.shape[0]
    cost = 0.0
    for i in range(m):
        z_i = np.dot(X[i],w)+b
        g_wb_i = sigmoid(z_i)
        cost += -y[i]*np.log(g_wb_i) - (1-y[i])*np.log(1-g_wb_i)
    cost = cost/m
    return cost

梯度计算函数（求偏导）

公式：

\(\frac{\partial J(\vec w,b)}{\partial b} = \frac{1}{m}\sum_{i=0}^{m-1}(g_{\vec w,b}(\vec x^{(i)})-y^{(i)})x_j^{(i)}\)

\(\frac{\partial J(\vec w,b)}{\partial b} = \frac{1}{m}\sum_{i=0}^{m-1}(g_{\vec w,b}(\vec x^{(i)})-y^{(i)})\)

其中，\(g_{\vec w,b}(x) = sigmoid(\vec w\cdot \vec x+b)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def compute_gradient_logistic(X, y, w, b):
    '''

    :param X: 特征集，矩阵
    :param y: 目标值，列表
    :param w: 向量
    :param b: 标量
    :return:
        dj_dw: 对数损失函数对向量w的偏导
        dj_db: 对数损失函数对b的偏导
    '''
    m,n = X.shape
    dj_dw = np.zeros((n,))
    dj_db = 0.0

    for i in range(m):
        g_wb_x = sigmoid(np.dot(X[i],w)+b)
        dj_db = dj_db + g_wb_x - y[i]
        for j in range(n):
            dj_dw[j] = dj_dw[j] + (g_wb_x - y[i])*X[i,j]
    dj_dw = dj_dw/m
    dj_db = dj_db/m

    return dj_dw,dj_db

梯度迭代函数

公式：

\(w_j = w_j - a\frac{\partial J(\vec w,b)}{\partial w_j},\quad j = 0,1,...,n-1\)

\(b = b - a\frac{\partial J(\vec w,b)}{\partial b}\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def logistic_regression(X_train,y_train,alpha,num_iters):
    '''

    :param X_train: 特征集，矩阵
    :param y_train: 目标值，列表
    :param alpha: 学习率，标量
    :param num_iters: 训练次数，标量
    :return:
        w: 训练得出的w，向量
        b: 训练得出的b，标量
    '''
    m,n = X_train.shape
    init_w = np.zeros((n,)) # n个特征，所以w有n个
    init_b = 0
    w = copy.deepcopy(init_w)
    b = init_b
    for i in range(num_iters):
        if i%100 == 0:
            print(i)
        dj_dw,dj_db = compute_gradient_logistic(X_train,y_train,w,b)
        w = w - alpha*dj_dw
        b = b - alpha*dj_db

    return w,b

训练数据集，绘制拟合决策边界

1
2
3
4
5
6
7
model_w,model_b = logistic_regression(X_train,y_train,alpha=0.4,num_iters=10000)
x_line = np.c_[np.arange(-4,4,0.1).reshape(-1,1),np.arange(-4,4,0.1).reshape(-1,1)]
print(model_w)
y_line = np.dot(x_line,model_w)+model_b

plt.plot(x_line,y_line,label = 'Predicted Value')
plt.show()

这是当训练次数为10000时得出的决策边界：

模型预测和评价

算出\(\vec w,b\)后，代入\(sigmoid(\vec w\cdot\vec x+b)\)，阈值为0.5。大于等于0.5为1类，小于0.5为0类。

注意要先将特征测试集标准化。

这里使用F1-Score（F1分数）进行评价。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 模型预测
def  model_predict(X,w,b):
    '''

    :param X: 测试集
    :param w: 向量
    :param b: 标量
    :return: 预测值（列表）
    '''
    y = []
    for i in X:
        if sigmoid(np.dot(i,w)+b) >= 0.5:
            y.append(1)
        else:
            y.append(0)
    return y
1
2
3
4
5
# 模型预测
X_test = (X_test - mu) / sigma
y_predict = model_predict(X_test,model_w,model_b)
f1_score = f1_score(y_test,y_predict,average='binary')
print(f"F1分数为:{round(f1_score,2)}")

结果：

补充：现在将特征集扩大到所有

直接上结果：

稍微比原来准确了一丢丢。

补充：使用sklearn完成逻辑回归

前面讲了一大堆，实际上sklearn几行代码搞定~

泪目

还是刚才那个数据（扩大到所有特征后的），直接上代码!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import pandas as pd
import numpy as np
import math,copy
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import f1_score
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler

data = pd.read_excel(r'.\Pumpkin_Seeds_Dataset\Pumpkin_Seeds_Dataset.xlsx', 0)
df = pd.DataFrame(data)
label = []
for i in df['Class']:
    if i == 'Çerçevelik':
        label.append(0)
    elif i == 'Ürgüp Sivrisi':
        label.append(1)

X_features_bk = np.array(df)
X_features = X_features_bk[:,:-1]
X_features = np.float32(X_features)
Y_target = np.array(label)

# 拆分训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(X_features,Y_target,train_size=0.5,random_state=45)

# 使用sklearn进行Z-score标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)  # 标准化训练集X

# 绘制训练集
color = []
for i in y_train:
    if i == 1:
        color.append("blue")
    else:
        color.append("orange")
plt.scatter(X_train[:, 2], X_train[:, 3], color=color)
plt.xlabel('Major_Axis_Length')
plt.ylabel('Minor_Axis_Length')
plt.show()

# 训练逻辑回归模型
lr_model = LogisticRegression()
lr_model.fit(X_train,y_train)

# 标准化测试集x
# 只有训练集才fit_transform，测试集是transform，原因上面自己写代码的时候说过了
X_test = scaler.transform(X_test)
# 预测
y_pred = lr_model.predict(X_test)
# F1-Score评估
f1_score = f1_score(y_test,y_pred,average='binary')
print(f"F1分数为:{round(f1_score,2)}")

中间我们拿出之前那两列来画了下图，这个图是同样的随机种子，采用sklearn的Z-score标准化后得出的图像：

对比我们之前自己处理的数据，只能说，完全一致好吧。

然后来看看结果：

甚至比我们自己写的差了这么一丢丢。导致这个的原因是它的学习率和训练次数和我们选的不一样，不过计算速度比我们快很多，我估计它训练次数选的比较少。如果我们调整自己的参数，也可以达到同样的效果！