过拟合与正则化

前言：这篇文章皆以回归模型为例。

在开始之前，你可能先要了解以下几个概念：

前置知识

偏差与方差

在机器学习中，偏差描述的是根据样本拟合出的模型输出结果与真实结果的差距，损失函数就是依据模型偏差的大小进行反向传播的。降低偏差，就需要复杂化模型，增加模型参数，但容易造成过拟合。方差描述的是样本上训练出的模型在测试集上的表现，降低方差，继续要简化模型，减少模型的参数，但容易造成欠拟合。根本原因是，我们总是希望用有限的训练样本去估计无限的真实数据。假定我们可以获得所有可能的数据集合，并在这个数据集上将损失函数最小化，则这样的模型称之为“真实模型”。但实际应用中，并不能获得且训练所有可能的数据，所以真实模型一定存在，但无法获得。欠拟合_百度百科 (baidu.com)

泛化能力

通俗来讲，就是训练出的模型对新鲜样本的适应能力。

什么是欠拟合与过拟合

示例：正常拟合情况

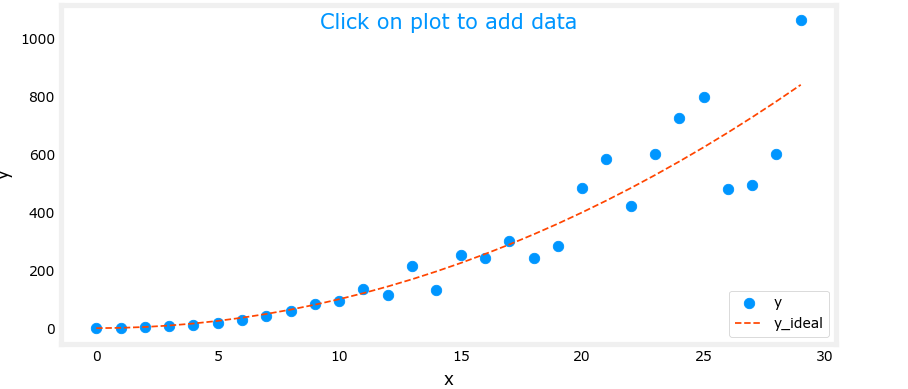
欠拟合：表现为高偏差。欠拟合模型在训练集、验证集和测试集表现均不佳。就像一个不好好学习的学生，在模拟考试和新的考试都考不好。

过拟合：表现为高方差。过拟合模型在训练集上表现很好，但遇到陌生数据时就表现得很差，即模型的泛化能力很差。就像一个学生在做模拟卷时太过于努力了，但是他学会的太贴合模拟卷的题型，但是遇到新的考试就做的很差。

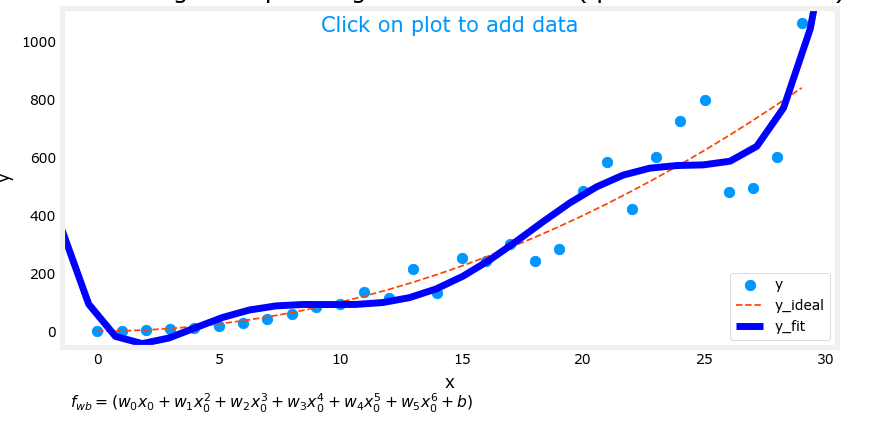
下图是逻辑回归的过拟合示例：

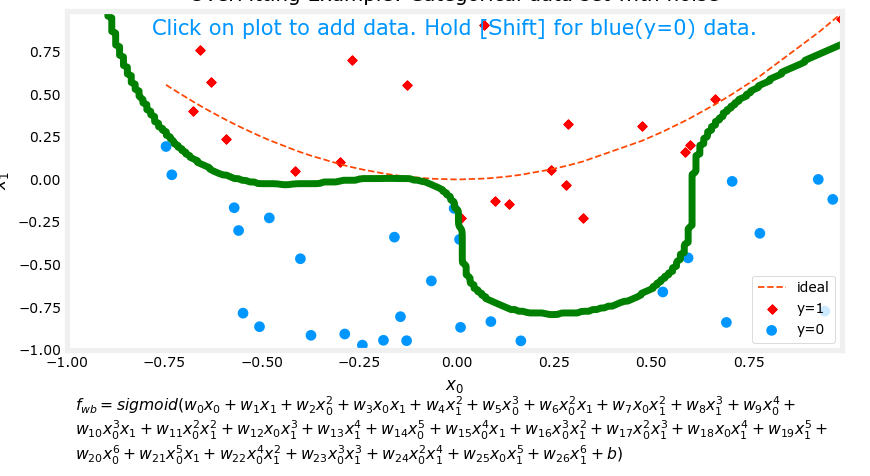
注：红线为正常拟合情况

导致欠拟合与过拟合的原因

欠拟合（underfitting）：

  • 特征量太少

  • 模型复杂度过低

过拟合（overfitting）： 这里只讨论回归模型的过拟合原因

  • 样本数量太少

  • 模型复杂度过高

  • 特征量太多

  • 样本的噪音数据干扰过大

解决方法

欠拟合：

相对较好解决。

  1. 选择更复杂的模型

  2. 增加更多特征

  3. 调整学习率、训练次数等参数

过拟合：

  1. 增加训练数据量，数据量越多，过拟合可能越小

  2. 减小模型复杂度。

  3. 减少特征数目。去除某些特征，可以提高模型泛化能力。

  4. 正则化（推荐）

正则化

这里只对线性回归和逻辑回归的正则化进行说明，其他模型和范数暂不拓展。

现在有下（右图）的过拟合模型

一种解决过拟合的方式是，我们可以手动筛选特征，直接将\(x^3,x^4\)去除。于是我们可以得到左边的模型。但还有一种不那么暴力的方法，我们如果可以让\(w_3,w_4\)尽量小，比如0.0000001，那么就相当于消除了\(x^3,x^4\)。

这是原来的代价函数：

\(J(\vec w,b) = \frac{1}{2m}\sum_{i=1}^{m}(f_{\vec w,b}(\vec x^{(i)})-y^{(i)})^2\)

现在，我们让\(J(\vec w,b)+1000w_3^2+1000w_4^2\)，如果要让现在的代价函数尽量小，\(w_3,w_4\)必须足够小。否则代价函数会非常非常大。于是我们就可以求得很小很小的\(w_3,w_4\)，有效的消除了\(x^3,x^4\)这两项特征的影响。

上面这个例子就是正则化的思想，我们正则化了\(x^3,x^4\)两个特征。

然而，实际中我们可能有许多种特征，比如100个特征，我们可能分不清哪些特征是重要的，哪些应该被正则化。

所以正则化一般的实现方式是正则化所有特征。不过一般不会正则化常数b。

正则化后的线性回归代价函数：

\(J(\vec w,b) = \frac{1}{2m}\sum_{i=1}^{m}(f_{\vec w,b}(\vec x^{(i)})-y^{(i)})^2+\frac{\lambda}{2m}\sum_{j = 0}^{n-1}w_j^2\)

当\(\lambda\)过小时，正则化效果较差。比如等于0时没有正则化。当\(\lambda\)过大时，可能会发生欠拟合。比如\(\lambda = 10^{10}\)，拟合出来的可能是一条几乎平行于x轴的直线\(f(x) = b\).

正则化后的线性回归和逻辑回归

代价函数

线性回归

公式：\(J(\vec w,b) = \frac{1}{2m}\sum_{i=1}^{m}(f_{\vec w,b}(\vec x^{(i)})-y^{(i)})^2+\frac{\lambda}{2m}\sum_{j = 0}^{n-1}w_j^2\)

其中，\(f_{\vec w,b}(x^{(i)}) = \vec w\cdot\vec x^{(i)}+b\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 线性回归正则化代价函数
def compute_cost_linear_reg(X, y, w, b, lambda_ = 1):
    '''

    :param X(narray(m,n)): m个样例，n个特征
    :param y(ndarray (m,)):目标值
    :param w(ndarray (n,)):模型参数
    :param b(scalar):模型参数
    :param lambda_(scalar):正则化控制量
    :return:
        total_cost (scalar):  损失值
    '''

    m,n = X.shape
    cost = 0.0
    for i in range(m):
        f_wb_i = np.dot(X[i],w) + b
        cost = cost + (f_wb_i - y[i])**2
    cost = cost / (2*m)

    reg_cost = 0
    for j in range(n):
        reg_cost += w[j]**2
    reg_cost = (lambda_/(2*m)) * reg_cost

    total_cost = cost + reg_cost
    return total_cost

逻辑回归

公式：

\(J(\vec w,b) = \frac{1}{m}\sum_{i=0}^{m-1}[-y^{(i)}log(f_{\vec w,b}(\vec x^{(i)})-(1-y^{(i)})log(1-f_{\vec w,b}(\vec x^{(i)})]+\frac{\lambda}{2m}\sum_{j = 0}^{n-1}w_j^2\)

其中，

\(f_{\vec w,b}(\vec x^{(i)}) = sigmoid(\vec w \cdot \vec x+b)\)

\(sigmoid(z) = \frac{1}{1+e^{-z}}\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def sigmoid(z):
    '''

    :param z: 标量
    :return: 标量
    '''
    g = 1 / (1 + np.exp(-z))
    return g   


# 逻辑函数正则化代价函数
def compute_cost_logistic_reg(X, y, w, b, lambda_ = 1):
    '''

    :param X(narray(m,n)): m个样例，n个特征
    :param y(ndarray (m,)):目标值
    :param w(ndarray (n,)):模型参数
    :param b(scalar):模型参数
    :param lambda_(scalar):正则化控制量
    :return:
        total_cost (scalar):  损失值
    '''
    m, n = X.shape
    cost = 0.0
    for i in range(m):
        z_i = np.dot(X[i], w) + b
        f_wb_i = sigmoid(z_i)
        cost += -y[i] * np.log(f_wb_i) - (1 - y[i]) * np.log(1 - f_wb_i)

    cost = cost / m

    reg_cost = 0
    for j in range(n):
        reg_cost += (w[j] ** 2)
    reg_cost = (lambda_ / (2 * m)) * reg_cost

    total_cost = cost + reg_cost
    return total_cost

梯度计算（求偏导）

线性回归和逻辑回归的梯度计算出来格式都一样，注意里面的\(f_{\vec w,b}(\vec x)\)指代不同即可。

公式：\(\frac{\partial J(\vec w,b)}{\partial b} = \frac{1}{m}\sum_{i=0}^{m-1}(f_{\vec w,b}(\vec x^{(i)})-y^{(i)})x_j^{(i)}+\frac {\lambda}{m}w_j\)

\(\frac{\partial J(\vec w,b)}{\partial b} = \frac{1}{m}\sum_{i=0}^{m-1}(f_{\vec w,b}(\vec x^{(i)})-y^{(i)})\)

线性回归中,\(f_{\vec w,b}(\vec x^{(i)}) = \vec w \cdot \vec x+b\)

逻辑回归中,\(f_{\vec w,b}(x) = sigmoid(\vec w\cdot \vec x+b)\)

线性回归：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def compute_gradient_linear_reg(X, y, w, b, lambda_):
    '''

    :param X(narray(m,n)): m个样例，n个特征
    :param y(ndarray (m,)):目标值
    :param w(ndarray (n,)):模型参数
    :param b(scalar):模型参数
    :param lambda_(scalar):正则化控制量
    :return:
        dj_dw (ndarray (n,)): 代价函数对w的偏导
        dj_db (scalar): 代价函数对b的偏导
    '''
    m, n = X.shape 
    dj_dw = np.zeros((n,))
    dj_db = 0.

    for i in range(m):
        err = (np.dot(X[i], w) + b) - y[i]
        for j in range(n):
            dj_dw[j] = dj_dw[j] + err * X[i, j]
        dj_db = dj_db + err
    dj_dw = dj_dw / m
    dj_db = dj_db / m

    for j in range(n):
        dj_dw[j] = dj_dw[j] + (lambda_ / m) * w[j]

    return dj_db, dj_dw

逻辑回归：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 逻辑回归梯度计算
def compute_gradient_logistic_reg(X, y, w, b, lambda_):
    '''

    :param X(narray(m,n)): m个样例，n个特征
    :param y(ndarray (m,)):目标值
    :param w(ndarray (n,)):模型参数
    :param b(scalar):模型参数
    :param lambda_(scalar):正则化控制量
    :return:
        dj_dw (ndarray (n,)): 代价函数对w的偏导
        dj_db (scalar): 代价函数对b的偏导
    '''

    m, n = X.shape
    dj_dw = np.zeros((n,))
    dj_db = 0.0

    for i in range(m):
        f_wb_i = sigmoid(np.dot(X[i], w) + b)
        err_i = f_wb_i - y[i]
        for j in range(n):
            dj_dw[j] = dj_dw[j] + err_i * X[i, j]
        dj_db = dj_db + err_i
    dj_dw = dj_dw / m
    dj_db = dj_db / m

    for j in range(n):
        dj_dw[j] = dj_dw[j] + (lambda_ / m) * w[j]

    return dj_db, dj_dw

梯度迭代就不写了，之前的文章有详细写过，没什么变化。

使用正则化后过拟合模型的变化

这是正则化之后的结果：

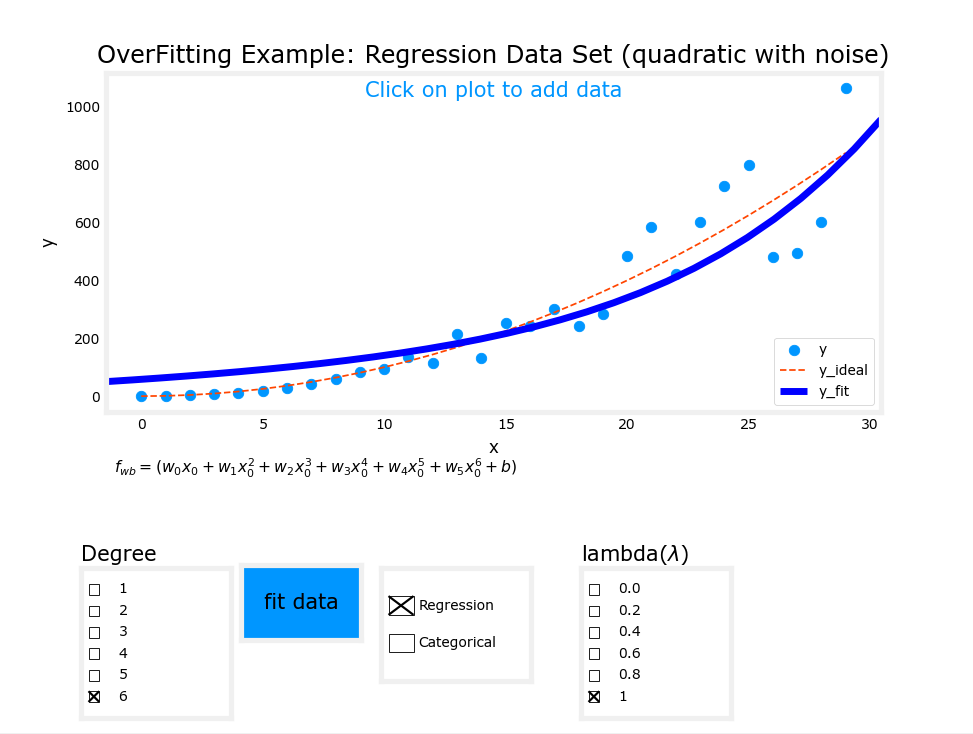
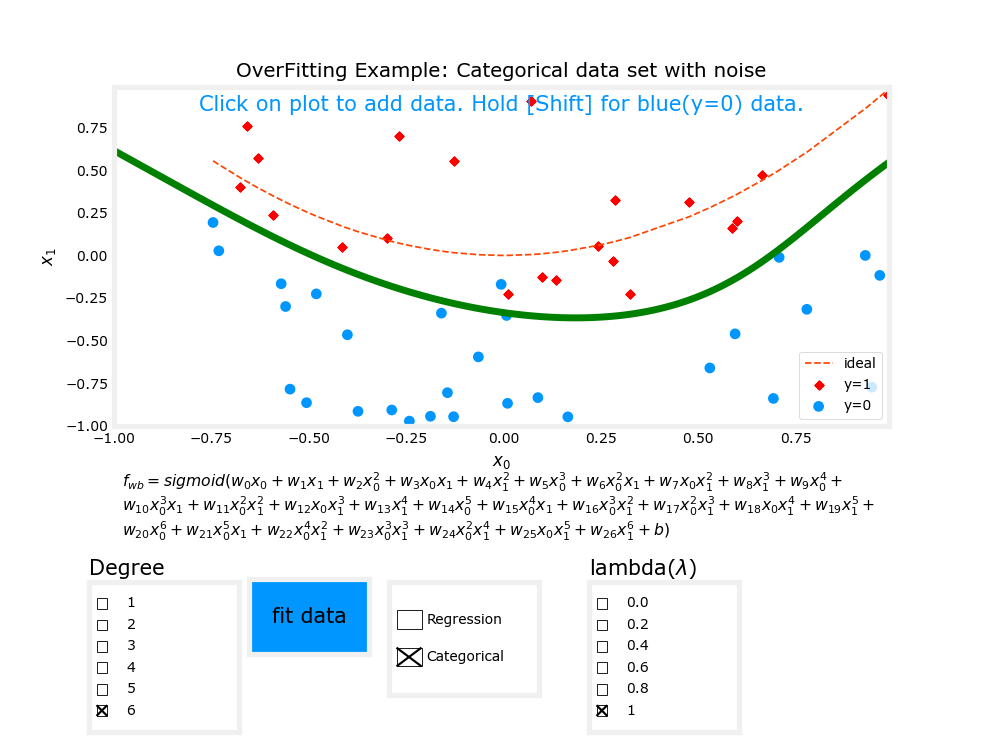
嗯...对比最开始的两张过拟合，已经好得多了，虽然比起红线模拟的模型还是有一些差距。