机器学习笔记10——EM算法原理与详细推导
本文章为EM算法笔记,本人学习和参考的文章:如何通俗理解EM算法_v_JULY_v的博客-CSDN博客_em算法
在开始之前,我们需要先复习一些在概率统计中学过的东西。
似然函数
统计学中,似然函数是一种关于统计模型参数的函数。给定输出x时,关于参数θ的似然函数L(θ|x)(在数值上)等于给定参数θ后变量X的概率:
L(θ|x)=P(X=x|θ)。
注:L(θ|x)也可以写为L(θ:x)
用例说明可能会更好理解:
考虑一个抛硬币实验,每次抛硬币相互独立,我们先假设正面朝上的概率\(P(H) = 0.5\) ,那么两次正面朝上的概率就是:
\(P(H,H) = 0.5\times 0.5 = 0.25\)
现在换一种角度,已知“两次抛硬币都是正面朝上”,则硬币正面朝上的概率为0.5的似然就是:
\(L(p(H) = 0.5;HH) = P(HH|P(H) = 0.5) = 0.25\)
同理,硬币正面朝上的概率为0.6的似然就是0.36。
极大似然估计(Maximum Likelihood Estimate,MLE)
极大似然估计也称为最大似然估计。
比如现在有一个袋子,里面装有白球和红球,你在里面随机抓了10个球,发现9个都是红球,那么你可以猜测从这个袋子抓出红球的概率为0.9,而抓出白球的概率为0.1。也就是说,我们根据样本来推测“为什么抓出来的样本会是这样”最可能的原因。
这种根据样本推断最可能的模型未知参数的方法叫做极大似然估计。
回到上面那个抛硬币的例子:如果两次抛硬币都是正面朝上。我们已经计算了当\(P(H) = 0.5\) 时,似然函数等于0.25;当\(P(H) = 0.6\) 时,似然函数等于0.36。计算\(P(H) = 1\)时,似然函数将会等于1,此时是最大的。
那么“两次抛硬币都正面朝上”的实验推出的极大似然估计就是“硬币正面朝上的概率为1”。
极大似然估计应用
现在我们使用抽样统计的方法从一个学校里随机抽取了100名男生和100名女生,并且统计他们各自的身高。
假设男生的身高服从高斯分布\(X \sim N(\mu_1,\sigma_1^2)\) ,女生身高服从另一个高斯分布\(X \sim N(\mu_2,\sigma_2^2)\) 。不过我们只知道他们服从高斯分布模型,并不知道这两个模型的各个参数,即\(\mu,\sigma\)
是未知参数。
现在,设\(\theta = [\mu,\sigma]^T\)。我们需要利用极大似然估计,通过100个男生样本和100个女生样本分别估计各自的\(\theta\) 。因为求男生和求女生的过程一样,只是样本不同。所以接下来仅以求解男生身高对应的极大似然估计为例。
令\(x_i\)为来自男生样本集X的第i个样本。现在套入之前提到的似然函数\(L(\theta)\):
$L() = P(X=x|θ)= P(x_1,x_2,...,x_n|) = _{i=1}^nP(x_i|) $
现在要求\(\hat\theta\) 使得似然函数\(L(\theta)\) 最大,求得的\(\hat\theta\) 即\(\theta\)的极大似然估计。用公式写出来就是:
\(\hat \theta = argmaxL(\theta)\)
求解极大似然估计
将似然函数化为对数似然函数:
\(\ell(\theta) = lnL(\theta) = ln\prod_{i=1}^nP(x_i|\theta) = \sum_{i=1}^nlnP(x_i|\theta)\)
转化成对数似然函数后,再求导(或偏导),令导数为0,解得的参数就是极大似然估计。
求解极大似然估计的一般步骤:
写出似然函数
化位对数似然函数
求导数,令导数为0,得到似然方程
求解似然方程
这里顺带提一下最大似然估计的适用条件:
1.样本独立同分布
2.已知样本服从某种分布模型,只是参数未知
以上都是概率统计的内容复习,及如何通过已知服从单个概率模型的样本集求解该模型的未知参数。
初识EM算法
问题引入
刚才提到,要想使用极大似然估计,必须确保样本都服从同一个分布。比如,我们通过100个男生身高样本使用极大似然估计可以算出男生身高服从的高斯模型。
现在,考虑这样一种情况:男女生的样本混合在一起了,你不知道这200个样本哪个是男生,哪个是女生。现在要想计算男女生各自服从的高斯模型的未知参数,就需要用到EM算法。
隐变量
像上述问题中这种“不知道样本属于男生还是女生”在EM算法中被称为隐变量。隐变量记作Z,样本i的隐变量记作\(z_i\)。
隐变量指不可观测数据,比如聚类中,训练样本集给出了特征却没给出类别。这时候样本的类别就是隐变量。
一般用Y表示可观测到的随机变量的数据,Z表示不可观测的随机变量的数据。Y与Z合起来被称为完全数据,只有Y则被称作不完全数据。
直观理解EM算法
假设有5枚硬币,这些硬币来自A,B两类,但我们不知道它们各自属于哪类硬币。现在把这5枚硬币各抛10次,请根据样本数据推测A,B两类硬币各自的“正面朝上的极大似然估计”,并且将这5枚硬币分类。
那么在上述例子中,“硬币种类”就是我们的隐变量,设为向量Z,\(Z = (z_1,z_2,z_3,z_4,z_5)\)
(注:H代表正面朝上,T代表反面朝上)
| 硬币序号 | 硬币类别 | 结果(X) | 统计 |
|---|---|---|---|
| 1 | \(z_1\),未知 | H T T T T H T T T T | 2H,8T |
| 2 | \(z_2\),未知 | H H H H T H H H H H | 9H,1T |
| 3 | \(z_3\),未知 | H T H T H H T T H H | 6H,4T |
| 4 | \(z_4\),未知 | T H T T H T T T H T | 3H,7T |
| 5 | \(z_5\),未知 | T H H H T H H H T H | 7H,3T |
现在使用EM算法求解:
step1:随机初始化模型参数\(\theta^{(0)}\) .
\(P(H_A)\)、\(P(H_B)\)分别是A类硬币、B类硬币正面朝上的概率,即模型未知参数\(\theta\)。
EM算法需要设置一个初始化模型参数\(\theta^{(0)}\) ,进而推出在\(\theta^{(0)}\) 条件下的隐变量Z。
设\(P(H_A) = 0.2\) , \(P(H_B) = 0.7\) 。
step2:计算隐变量
计算各硬币的隐变量:
还记得最开始提到的似然函数吗?这里就需要求似然,即\(L(θ|x)=P(X=x|θ)\)。
例:
对于1号硬币,属于A类的似然:
\[ \begin{split} L(\theta_A^{(0)}|X = x_1)&= P(X = x_1|\theta_A^{(0)}) \\&= \prod_{j = 1}^{10}P(x_{1,j}|\theta_A^{(0)})\\&= 0.2^2\times0.8^8 = 67.1089\times10^{-4}\end{split} \]
对于1号硬币,属于B类的似然:
\[ \begin{split}L(\theta_B^{(0)}|X = x_1)& = P(X = x_1|\theta_B^{(0)}) \\&= \prod_{j = 1}^{10}P(x_{1,j}|\theta_B^{(0)})\\&= 0.7^2\times0.3^8 = 0.3215*10^{-4}\end{split} \]
比较属于A类和属于B类的似然,发现A的似然更大,则把1号硬币归为A类,即令隐变量\(z_1 = A\)。
各枚硬币的隐变量计算:
| 序号 | 统计 | A类的似然(\(10^{-4}\)) | B类的似然(\(10^{-4}\)) | 类别(隐变量) |
|---|---|---|---|---|
| 1 | 2H,8T | 67.11 | 0.32 | \(z_1\) = A |
| 2 | 9H,1T | 0.004 | 121.06 | \(z_2\) = B |
| 3 | 6H,4T | 0.26 | 9.53 | \(z_3\) = B |
| 4 | 3H,7T | 16.78 | 0.75 | \(z_4\) = A |
| 5 | 7H,3T | 0.06 | 22.24 | \(z_5\) = B |
我们通过假设模型未知参数,“猜出了”硬币各自属于哪一类,使得隐函数变为已知值,这时就满足了应用极大似然估计的条件,于是可以用极大似然估计求解未知参数\(\theta^{(1)}\)。
step3:极大似然估计求解模型参数\(\theta^{(1)}\) .
根据\(\theta^{(0)}\) ,我们算出了1号、4号属于A类,2、3、5属于B类。于是跟新\(P(H_A)\)和\(P(H_B)\):
\(P(H_A) = \frac{2+3}{20} = 0.25\)
\(P(H_B) = \frac{9+6+7}{30} = 0.73\)
可以看出\(\theta^{(1)}\)与\(\theta^{(0)}\) 并不相同。聪明的你可能想到了,接下来就是迭代的过程,重复step2和step3得到\(\theta^{(2)}\)、\(\theta^{(3)}\) ...
可以证明,模型参数会随着迭代越来越接近真实值,并且一定会收敛到局部最优值。但不一定会收敛到全局最优值。
隐变量的期望(隐变量的概率分布)
通过初步认识EM算法,你已经大致知道EM算法在干嘛了,但是EM算法在处理隐变量时,并不是通过似然函数判断某个样本的隐变量属于哪一个特定值,而是求隐变量的概率分布。再通过隐变量的概率分布进行后续运算。所以在正式开始推导EM算法前,我们还需要知道隐变量的概率分布。
隐变量的概率分布
我们使用期望来简化计算,于是求隐变量的概率分布就是隐变量的期望。因为上面那个抛硬币的数据算出来的期望比较极端,所以这里重新举一个例子:现在有五枚硬币,分别来自A,B两类,但分类未知。
| 硬币序号 | 结果 | 统计 |
|---|---|---|
| 1 | H H T H T | 3H,2T |
| 2 | T T H H T | 2H,3T |
| 3 | H T T T T | 1H,4T |
| 4 | H T T H H | 3H,2T |
| 5 | T H H T T | 2H,3T |
因为前面的过程都一样,所以我们直接来到计算出极大似然这一步。现在已经在随机固定模型参数\(\theta^{(0)}\) 的情况下计算出了每一枚硬币对应的似然:
| 硬币序号 | A类似然 | B类似然 |
|---|---|---|
| 1 | 0.00512 | 0.03087 |
| 2 | 0.02048 | 0.01323 |
| 3 | 0.08192 | 0.00567 |
| 4 | 0.00512 | 0.03087 |
| 5 | 0.02048 | 0.01323 |
在上一节中,接下来我们直接确认了隐变量的值。现在,我们用隐变量的期望来计算隐变量的概率分布\(Q(z)\) 。
因为每一个样本都有自己的隐变量概率分布,所以精确到样本的隐变量概率分布应该写为:\(Q_i(z^{(i)})\)。\(z^{(i)}\) 表示这是第\(i\) 个样本的隐变量。
例如硬币1的隐变量概率分布:
$ P(z_1=A) = = 0.14$
\(P(z_1=B) = 1-0.14 = 0.86\)
其他同理,隐变量的期望如下:
| 硬币序号 | P(\(z_i\) = A) | \(P(z_i=B)\) |
|---|---|---|
| 1 | 0.14 | 0.86 |
| 2 | 0.61 | 0.39 |
| 3 | 0.94 | 0.06 |
| 4 | 0.14 | 0.86 |
| 5 | 0.61 | 0.39 |
再将隐变量的分布函数代入最开始的表以计算极大似然估计来计算下一轮的模型参数\(\theta^{(1)}\) ,即新的\(P(H_A)\)、\(P(H_B)\)。
计算1号各权值:
1号是A类时正面朝上的权值: $w(A_1 = H) = 3*0.14 = 0.42 $
1号是A类时反面朝上的权值:\(w(A_1 = T) = 2*0.14 = 0.28\)
1号是B类时正面朝上的权值:\(w(B_1 = H) = 3*0.86= 2.58\)
1号是B类时反面朝上的权值:\(w(B_1 = T) = 2*0.86 = 1.72\)
| 序号 | 统计 | \(w(A_i = H)\) | \(w(A_i = T)\) | \(w(B_i=H)\) | \(w(B_i = T)\) |
|---|---|---|---|---|---|
| 1 | 3H,2T | 3*0.14 = 0.42 | 2*0.14 = 0.28 | 3*0.86 = 2.58 | 2*0.86 = 1.72 |
| 2 | 2H,3T | 2*0.61 = 1.22 | 3*0.61 = 1.83 | 2*0.39 = 0.78 | 3*0.39 = 1.17 |
| 3 | 1H,4T | 1*0.94 = 0.94 | 4*0.94 = 3.76 | 1*0.06 = 0.06 | 4*0.06 = 0.24 |
| 4 | 3H,2T | 3*0.14 = 0.42 | 2*0.14 = 0.28 | 3*0.86 = 2.58 | 2*0.86 = 1.72 |
| 5 | 2H,3T | 2*0.61 = 1.22 | 3*0.61 = 1.83 | 2*0.39 = 0.78 | 3*0.39 = 1.17 |
| 总权值 | 4.22 | 7.98 | 6.78 | 6.02 |
\(\theta^{(1)}:\)
\(P(H_A) = \frac{4.22}{4.22+7.98} = 0.35\)
\(P(H_B) = \frac{6.78}{6.78+6.02} = 0.52\)
这就是使用隐变量概率分布求极大既然估计的过程。
现在推广到一般情况:
EM算法公式详细推导
含隐变量的对数似然函数
之前我们提到,极大似然估计是为了求下面这个似然函数的极大值: $ L() = P(X=x|θ)= P(x_1,x_2,...,x_n|) = _{i=1}^nP(x_i|)$
其中,X服从独立同分布,\(\theta\)为概率分布模型参数。
根据极大似然方程的步骤,要先将似然函数化为对数似然函数: \[ \begin{split} &\ell(\theta)= logL(\theta) = log\prod_{i=1}^nP(x_i|\theta) \\ & = \sum_{i=1}^nlogP(x_i|\theta)\end{split} \]
问题在于现在X并不是同分布的样本集,同分布样本需要由X和隐变量Z共同确定。于是引入隐变量Z的对数似然变为:
\[ \begin{split}\ell(\theta)& =\sum_{i=1}^nlogP(x_i|\theta) \\&= \sum_{i=1}^nlog\sum_{z}^{Z^{(i)}}P(x_i,z|\theta) \end{split} \]
这里解释一下\(P(x_i|\theta) = \sum_z^{Z^{(i)}}P(x_i,z|\theta)\):
此处为全概率公式,描述为:对每个样例的每种可能类别求联合分布概率和。
按照求极大似然的步骤,接下来对\(\ell(\theta)\)应该求偏导,然后令偏导为0,求解似然方程。但是这里多了个随机变量z,像\(log\sum\) 的形式求导太过于复杂,所以我们需要转化方程:
利用jensen不等式转化方程
待会儿解释jensen不等式是什么,先看转化结果。
为了使用jensen不等式,我们需要先把分子分母都乘隐变量\(z_i\)的概率分布函数\(Q_i(z^{(i)})\)。
然后通过jensen不等式,可以将其变为:
\[ \begin{split}\ell(\theta) = \sum_{i=1}^nlog\sum_{z}^{Z^{(i)}}P(x_i,z|\theta) (1)\\= \sum_{i=1}^nlog\sum_{z}^{Z^{(i)}}Q_i(z)\frac{P(x_i,z|\theta)}{Q_i(z)} (2)\\\geq \sum_{i=1}^n\sum_{z}^{Z^{(i)}}Q_i(z)log\frac{P(x_i,z|\theta)}{Q_i(z)} (3)\end{split} \]
(注:因为\(z\)来自于\(Z^{(i)}\),所以其实\(z\) 就是\(z^{(i)}\) 的简写。)
可以看出对于(3)式就很好求导了。
接下来说明是如何从(2)转化为(3)的。
jeasen不等式转化详解
(国际定义)凸函数:设\(f(x)\)为定义域为实数的函数。
对于所有实数x,若\(f''(x) \geq0\) ,则\(f(x)\)为凸函数。即下凹为凸,上凸为凹。
当x为向量,如果hessian矩阵H是半正定的(\(H\geq0\)),那么\(f(\vec x)\) 为凸函数。
若\(f''(x)>0\)或\(H>0\) ,则\(f(x)\)为严格凸函数。
Jeasen不等式:
如果f是凸函数,X是随机变量,那么:\(E[f(X)]>=f(E[X])\),通俗的说法是函数的期望大于等于期望的函数。而凹函数反之。
特别地,如果f是严格凸函数,当且仅当\(P(X = EX) = 1\)。即X是常量时,有\(E[f(X)] = f(EX)\)。
图就不画了,大概了解上述的用法即可。所以要用jeason不等式的关键在于,函数要为凸或凹函数,且需要表示出期望。
如何表示期望
通过将公式变成含有\(Q_i(z^{(i)})\)的式子。我们可以表示出期望:
如果你还记得期望公式的懒人定理:
设Y是关于随机变量X的函数,\(Y = g(X)\) ,g为连续函数,那么:
若X是离散型随机变量,X分布律为\(P(X = x_k) = P_k,k = 1,2,3...,\)若\(\sum_{k=1}^\infty g(x_k)p_k\) 绝对收敛则有:
\(E(Y) = E[g(X)] = \sum_{k=1}^\infty g(x_k)p_k\)
若X是连续型随机变量,X的概率密度为\(f(x)\),若\(\int_{-\infty}^\infty g(x)f(x)dx\) 绝对收敛,则有:
\(E(Y) = E[g(X)] = \int_{-\infty}^\infty g(x)f(x)dx\)
根据懒人定理,(2)中的\(\sum_{z}^{Z^{(i)}}Q_i(z)\frac{P(x_i,z|\theta)}{Q_i(z)}\) 就是\(\frac{P(x_i,z^{(i)}|\theta)}{Q_i(z^{(i)})}\) 的期望。原因:\(Q_i(z^{(i)})\) 是\(z^{(i)}\) 的分布函数,而\(\frac{P(x_i,z^{(i)}|\theta)}{Q_i(z^{(i)})}\) 是关于随机变量\(z^{(i)}\)的函数。
于是,令\(g(z^{(i)}) = \frac{P(x_i,z^{(i)}|\theta)}{Q_i(z^{(i)})}\),
则\(E(g(z^{(i)})) = \sum_{z}^{Z^{(i)}}Q_i(z)\frac{P(x_i,z|\theta)}{Q_i(z)}\) 。
为什么是凹函数
在(1)式中,将\(log\sum_{z}^{Z^{(i)}}P(x_i,z|\theta)\) 看作一个整体,即\(log(x)\) 。由于\(f''(log(x))<0\),所以是凹函数。
转化对数似然方程式为不等式
由于是凹函数,所以不等式反向:\(f(E[X])\geq E[f(x)]\),
令\(f(x) = logx\),\(X = g(z^{(i)})\)则:
\(f(E[X]) = f(E[g(z^{(i)})]) = log\sum_{z}^{Z^{(i)}}Q_i(z)\frac{P(x_i,z|\theta)}{Q_i(z)}\)
$E[f(X)] = E[f(g(z^{(i)}))] = _{z}{Z{(i)}}Q_i(z)log $ ;
于是:
\[ \begin{split}\ell(\theta) = \sum_{i=1}^nlog\sum_{z}^{Z^{(i)}}Q_i(z)\frac{P(x_i,z|\theta)}{Q_i(z)}\\ \geq \sum_{i=1}^n\sum_{z}^{Z^{(i)}}Q_i(z)log\frac{P(x_i,z|\theta)}{Q_i(z)} = J(z,Q)\end{split} \]
至此,我们得到了一个好求偏导的公式。
拔高下界
回顾我们的目标:使\(\ell(\theta)\) 最大化,直至目前,我们通过jensen不等式,获得了一个可以求导的公式\(J(z,Q)\)。现在的目的是通过\(J(z,Q)\)获得\(\ell(\theta)\) 最大值。
我们可以通过不断最大化\(J(z,Q)\)的下界来让\(\ell(\theta)\) 不断提高。为了顺利理清接下来的过程,在这里回顾一下各函数和变量的说明:
\(\theta\) : 模型参数(未知),我们可以假设它已知,并在不断迭代中更新\(\theta\) 。
\(\ell(\theta)\):对数似然方程,我们需要调整\(\theta\)使得\(\ell(\theta)\) 取极大值,此时$= argmax () $
\(Q(z)\):隐变量z的概率分布,其实就是隐变量的期望。
\(J(z,Q)\): 不等式右边的方程,我们可以不断调整它的最大值来使得\(\ell(\theta)\) 最大。
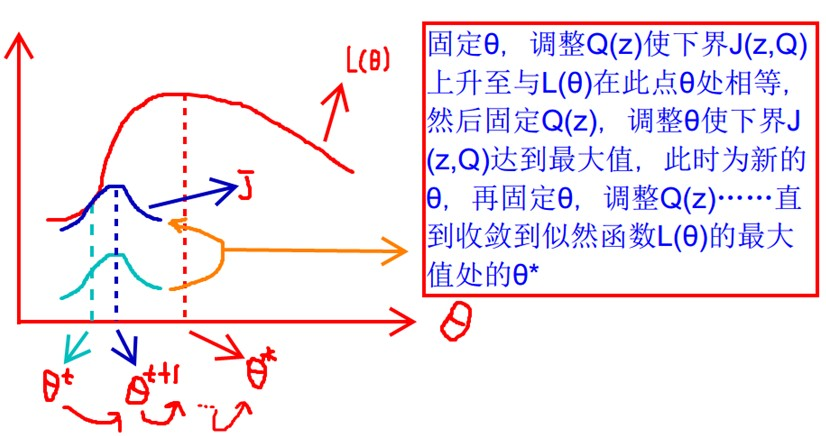
step1.首先固定\(\theta\) ,调整\(Q(z)\)使下界\(J(z,Q)\) 上升到与\(\ell(\theta)\) 在点\(\theta\) 处相等。
step2.固定\(Q(z)\),并使用极大似然估计法使\(\theta^{(t)}\)达到最大值\(\theta^{(t+1)}\) 。
step3.再将\(\theta^{(t+1)}\)固定为模型参数,重复以上过程,直至收敛达到\(\ell(\theta)\)最大值。此时对应的 \(\hat\theta\)即为所求。
关于EM算法一定收敛的证明过程就暂时不写了。
step1想解决的问题可以阐述为:在模型参数已知的情况下,隐变量的最可能概率分布是什么?答案:使得\(J(z,Q)\)与\(\ell(\theta)\)在\(\theta\)处相等的\(Q(z)\) 。
于是引出了新的问题:什么时候\(J(z,Q)\)才与\(\ell(\theta)\)相等?
什么时候\(J(z,Q) = \ell(\theta)\)
回顾Jensen不等式,当X是常量时,\(E[f(X)] = f(EX)\)。所以我们为了让\(J(z,Q) = \ell(\theta)\) ,需要让\(X\)为常数。
于是\(X = g(z^{(i)}) = \frac{P(x_i,z^{(i)}|\theta)}{Q_i(z^{(i)})} = c\) ,其中\(c\)为常数。
在由(1)变化(2)时,曾经提到过\(\sum_z^{Z^{(i)}}Q_i(z^{(i)}) = 1\)。因为\(Q(z)\)是隐变量z的概率分布,概率之和为1。
现在我们可以变换公式:(先同乘分母,再化简)
因为 :\(\frac{P(x_i,z^{(i)}|\theta)}{Q_i(z^{(i)})} = c\),
所以:\(\sum_z^{Z^{(i)}}P(x_i,z^{(i)}|\theta) = \sum_z^{Z^{(i)}}Q_i(z^{(i)})c = c\) ,即\(\sum_z^{Z^{(i)}}P(x_i,z^{(i)}|\theta) = c\) (1)
又因为由\(\frac{P(x_i,z^{(i)}|\theta)}{Q_i(z^{(i)})} = c\) 可得:
\(Q_i(Z^{(i)}) = \frac{P(x_i,z^{(i)}|\theta)}{c}\) (2)
于是当\(J(z,Q) = \ell(\theta)\)时,将(1)代入(2)可得:
\[ \begin{split}Q_i(Z^{(i)})& = \frac{P(x_i,z^{(i)}|\theta)}{c} \\ &=\frac{P(x_i,z^{(i)}|\theta)}{\sum_z^{Z^{(i)}}P(x_i,z^{(i)}|\theta)} \\ &= P(z^{(i)}|x_i;\theta)\end{split} \]
结论:
当\(J(z,Q) = \ell(\theta)\)时,\(Q_i(z^{(i)})\) 为隐变量的条件概率分布,即隐变量的期望。
现在我们只需要利用似然函数求隐变量的期望即可(前面有讲过怎么求)。
EM算法总结
EM算法应用场景
EM算法是一种迭代算法,主要用于含有隐变量的概率模型参数的极大似然估计或极大后验估计。广泛应用于缺损数据、截尾数据、成群数据、带有讨厌参数的数据等所谓不完全数据的统计推断问题。
EM算法步骤
其实在EM算法直观理解和详细推导时已经说了两次它的步骤了,不过在这里还是再总结一下,如果你和我一样没看懂,待会儿会给出解释:
输入:观测变量数据Y;隐变量数据Z;联合分布\(P(Y,Z|\theta)\),即完全数据的概率分布;条件分布\(P(Z|Y,\theta)\),即未观测数据Z的条件概率分布。
输出:模型参数\(\theta\) 。
step1:初始化模型参数\(\theta^{(0)}\) ,进入迭代。
step2(E-step):记\(\theta^{(i)}\) 为第i次迭代参数\(\theta\) 估计值,第\(i+1\)次迭代的E-step将计算
\[ \begin{split}Q(\theta,\theta^{(i)})=E_z[logP(Y,Z|\theta)|Y,\theta^{(i)}]\\ =\sum_ZlogP(Y,Z|\theta)P(Z|Y,\theta^{i}) \end{split} \]
step3(M-step):利用极大似然估计,计算使\(Q(\theta,\theta^{(i)})\) 极大化的\(\hat \theta\),作为第\(i+1\) 次迭代的参数估计值\(\theta^{(i+1)}\)。
\(\theta^{(i+1)} = argmax_\theta Q(\theta,\theta^{(i+1)})\)
step4:重复step2、step3直到收敛。收敛时的\(\theta\) 即为所求。
关于步骤的解释
\(Q(\theta,\theta^{(i)})\):完全数据的对数似然函数\(P(Y,Z|\theta)\) 关于在给定观测数据Y和当前参数\(\theta^{(i)}\) 下对未观测数据Z的条件概率分布\(P(Z|Y,\theta^{(i)})\) 的期望称为Q函数。
所以这个Q函数其实就是推导过程中的\(Q_i(z^{(i)})\) ,在拔高下界时详细说明了为什么求的是它。
也就是说,E-step求的是在固定\(\theta\) 的条件下求隐变量z的期望,等同于拔高下界中的step1。
而M-step则是固定\(Q_i(z^{(i)})\) 后极大似然估计求\(\theta^{(i+1)}\) 的过程。等同于拔高下界中的step2。
关于EM算法的重要说明
初始化时可以随机选择\(\theta^{(0)}\) ,但是EM算法对初始值很敏感,一旦选择不好会造成很大的计算损失。 对于初始值的选择也有相关的做法,这里暂时不研究。
停止迭代的条件一般是对于较小的正数\(A\) ,若满足\(|\theta^{(i+1)}-\theta^{(i)}|< A\) ,停止迭代。
EM算法的推进还有广义EM算法和EM算法变种等等。
算法优缺点
优点:
通常计算起来比较简单
收敛稳定,不需要设置超参数
缺点:
对大规模数据和多维高斯分布,计算量大,迭代速度慢
如果初始值设置不当,收敛过程的计算代价会非常大。
EM算法求得的是局部最优解而不一定是全局最优解。
EM算法的应用
关于EM算法的应用,例如处理混合高斯模型(GMM)和聚类等等,将会在下一篇EM文章中详细介绍。


