前言

之前在推GMM公式时有点问题但是自己没有发现，所以现在重新写一遍GMM的推导。这篇文章涉及EM算法的部分就不过多赘述，上篇文章已经推导过EM算法。

高斯混合模型简介

高斯混合模型（Gaussian Mixed Model）简称GMM，指多个高斯分布函数的线性组合，理论上GMM可以拟合出任意类型的分布。高斯混合模型通常用于解决同一集合下的数据包含多个不同的分布的情况，具体应用有聚类、密度估计、生成新数据等。

GMM与K-mean

根据K-mean聚类算法的原理，K-mean算法的缺点之一在于无法将两个聚类中心点相同的类进行聚类，比如$A\sim N(\mu,\sigma_1^2),B\sim N(\mu,\sigma^2_2)$ ,此时将无法用K-mean算法聚类出A，B。为了解决这一缺点，提出了高斯混合模型（GMM）。GMM通过选择成分最大化后验概率完成聚类，各数据点的后验概率表示属于各类的可能性，而不是判定它完全属于某个类，所以称为软聚类。其在各类尺寸不同、聚类间有相关关系的时候可能比k-means聚类更合适。

高斯混合模型的概率密度函数

下面将分别从几何模型角度和混合模型角度分别解释GMM的概率密度函数。

几何角度

假设我们现在有以下数据分布。

上述图像中，红色曲线为数据分布。可以发现，如果仅用图中任一单个高斯分布来表示红色曲线是不合适的。因此，我们可以将图中两个高斯分布进行加权平均得到一个新的分布。而这个分布就是高斯混合模型。

于是，从几何模型来看，GMM的概率密度函数可表示为若干个高斯分布的加权平均： \[ p(x) = \sum_{k=1}^N\alpha_kN(x|\mu_k,\Sigma_k),\sum_{k=1}^N\alpha_k=1 \] 上述公式中，$\alpha_k$ 为权值。

混合模型角度

这次我们来观察一个二维高斯混合模型数据分布。

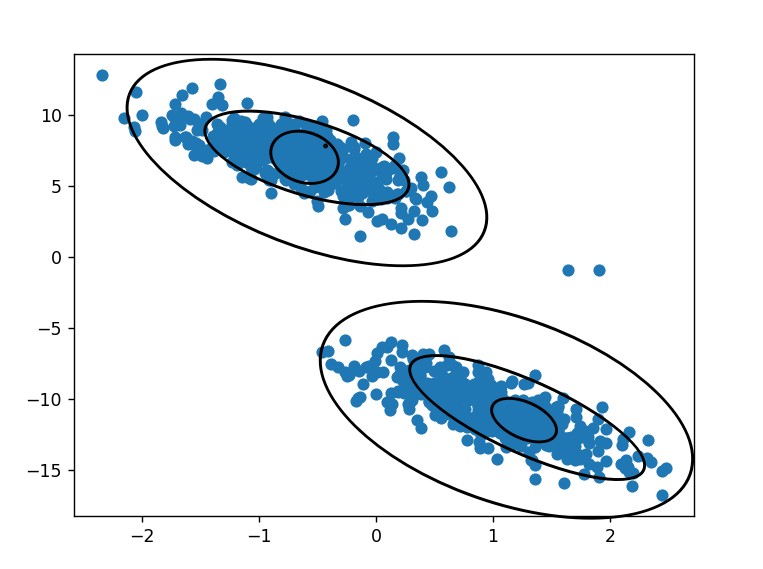
黑色线框为两个高斯分布的等高线（从上往下看的投影）。现在在图中任取一样本点，考虑它分别属于这两个高斯分布的概率。比如你可以说其中一个样本属于第一个高斯分布的概率为0.8，属于第二个高斯分布的概率为0.2。注意，这里说的是后验概率。

现在我们引入隐变量z，用于表示对应的样本属于哪一个高斯分布。有一点需要特别注意，对于每一个样本，都有自己的隐变量。或者说，z是对于个体而言而非整体而言的。

$z=c_i$表示样本属于第i类，$P(z=c_i)$是隐变量的概率分布。

$z$	$c_1$	$c_2$	...	$c_k$
$P$	$p_1$	$p_2$	...	$p_k$

引入隐变量z后，有： \[ \begin{split} p(x|\theta) &= \sum_{k=1}^Kp(x,z=c_k|\theta)\\ &= \sum_{k=1}^Kp(z=c_k|\theta)p(x|z=c_k,\theta)\\ &= \sum_{k=1}^KP_kN(x|\mu_k,\Sigma_k),\sum_{k=1}^KP_k=1 \end{split} \] 综合两个角度，高斯混合模型概率密度函数可以表示为：

几何角度：$p(x) = \sum_{k=1}^N\alpha_kN(x|\mu_k,\Sigma_k),\sum_{k=1}^N\alpha_k=1$
混合模型角度：$p(x|\theta) = \sum_{k=1}^KP_kN(x|\mu_k,\Sigma_k),\sum_{k=1}^KP_k=1$

可以看出，二者的表示是一样的。在几何角度中，$\alpha _k$表示权值；在混合模型角度中，$P_k$表示隐变量的概率分布。

可能会弄混的地方

隐变量的分布与隐变量的后验概率分布

我在这儿被绕晕了好久，也是重新写这篇文章的直接原因。
我主要是被隐变量的后验分布和隐变量的分布弄晕了，在这里记录一下。

回顾GMM中隐变量的含义是：某样本属于哪一类高斯分布。

因此M-step中，求隐变量的概率分布$a_k$类似抛硬币计算正面朝上的概率类似，比如抛10次硬币6次朝上。不过在EM算法中，隐变量并不通过个确定的值计算概率分布，而是通过隐变量后验概率分布计算的，这部分内容在上一篇文章（EM算法推导）中具体举例说明过。

而E-step中,求的是隐变量的后验概率分布，所以才会有每一个样本都对应一个隐变量的（后验）概率分布。

极大似然估计

该部分是为了引出EM算法，可以跳过。

现在我们要用已知样本估计k个高斯分布的参数，一般通过样本估计模型参数的方法为极大似然估计（MLE），MLE在EM算法中已经讲过。

回顾MLE目标函数: \[ \begin{split}\hat\theta& = argmax_\theta logP(X|\theta) \\ &= argmax_\theta log \prod_{i=1}^np(x_i|\theta)\\ &= argmax_\theta \sum_{i=1}^n logp(x_i|\theta)\end{split} \] 将高斯混合模型的概率密度函数代入，得： \[ \begin{split}\hat\theta &= argmax_\theta \sum_{i=1}^n logp(x_i|\theta)\\&=argmax_\theta\sum_{i=1}^nlog\sum_{k=1}^K\alpha_kN(x_i|\mu_k,\Sigma_k)\end{split} \] 因为引入了隐变量，导致这个式子含有$log\sum$ ，无法再进行MLE下一个步骤。回顾EM算法，EM算法就是拿来求解此类问题的。于是接下来需要用EM迭代求近似解。

EM算法求近似解

明确变量和参数

$X$：可观测数据集，$X = (x_1,x_2,...,x_n)$

$Z$：未观测数据集，$Z=(z_1,z_2,...,z_n)$

$\theta$：模型参数，$\theta = (\alpha,\mu,\Sigma)$

参数$\theta$包含隐变量z的概率分布，各个高斯分布的均值和协方差矩阵：

$\alpha = (\alpha_1,\alpha_2,...,\alpha_k)$

$\mu = (\mu_1,\mu_2,...,\mu_k)$

$\Sigma = (\Sigma_1,\Sigma_2,...,\Sigma_k)$

E-step

回顾EM算法，上一篇中我们推导出E-step实际上求的是隐变量的后验概率分布$p(z_i|x_i,\theta^{(t)})$。

为了便于表示，之后也将$p(z_i|x_i,\theta^{(t)})$表示为$\gamma_t(z^{(i)})$ 。将i变成上标的形式是为了之后便于将$z_i = c_k$简写为$z_k^{(i)}$。

隐变量的后验概率分布： \[ \begin{split} \gamma_t(z_j^{(i)}) &= p(z_i = c_j|x_i,\theta^{(t)})\\ & = \frac{p(x_i,z_i=c_j|\theta^{(t)})}{\sum_{k=1}^Kp(x_i,z_i=c_k|\theta^{(t)})}\\ &=\frac{p(x_i|z_i=c_j,\theta^{(t)})p(z_i=c_j|\theta^{(t)})}{\sum_{k=1}^Kp(x_i|z_i=c_k,\theta^{(t)})p(z_i=c_k|\theta^{(t)})}\\ &=\frac{\alpha_j^{(t)}N(x_i|\mu_j^{(t)},\Sigma_j^{(t)})}{\sum_{k=1}^Ka_k^{(t)}N(x_i|\mu_k^{(t)},\Sigma_k^{(t)})} \end{split} \]

简化Q函数

回顾E步的Q函数： \[ \begin{split}Q(\theta,\theta^{(t)})& = E_z[logP(X,Z|\theta)|X,\theta^{(t)}] \\&= \sum_ZlogP(X,Z|\theta)P(Z|X,\theta^{(t)})\end{split} \] 注：$_Z $ 是$\sum_{z_1,z_2,...,z_n}$的简写。

因为高斯混合模型中的完整数据$(X,Z)$ 独立同分布，未观测数据$Z$ 独立同分布，所以： \[ \begin{split}Q(\theta,\theta^{(t)}) &=\sum_Zlog \prod_{i=1}^n p(x_i,z_{i}|\theta)\prod _{i=1}^np(z_{i}|x_i,\theta^{(t)})\\&= \sum_Z[ \sum_{i=1}^nlog p(x_i,z_{i}|\theta) ]\prod _{i=1}^np(z_{i}|x_i,\theta^{(t)})\end{split} \]

关于最前面那个$\sum_Z$ 的解释：
如果是是连续型函数，Q的表达式应该是：
$Q(\theta,\theta^{(t)}) = \int_ZlogP(X,Z|\theta)P(Z|X,\theta^{(t)})dz$
但是现在是离散型，所以积分就变成了求和。

展开Q函数

\[ Q(\theta,\theta^{(t)}) = \sum_Z[ logp(x_1,z_{1}|\theta)+logp(x_2,z_{2}|\theta)+...+logp(x_n,z_{n}|\theta) ] \prod _{i=1}^np(z_{i}|x_i,\theta^{(t)}) \]

只看第一项 \[ \sum_Zlogp(x_1,z_{1}|\theta)\prod _{i=1}^np(z_{i}|x_i,\theta^{(t)}) \] 因为$logp(x_1,z_{1}|\theta)$ 只与$z_{1}$ 相关，而$\prod _{i=1}^np(z_{i}|x_i,\theta^{(t)})$中，$p(z_{1}|x_i,\theta^{(t)})$ 与$z_{1}$相关，所以可以将上式改写为： \[ \begin{split}&\sum_Zlogp(x_1,z_{1}|\theta)\prod _{i=1}^np(z_{i}|x_i,\theta^{(t)})\\&=\sum_{z_{1}}logp(x_1,z_{1}|\theta)p(z_{1}|x_1,\theta^{(t)})[\sum_{z_{2},...z_{n}}\prod _{i=2}^np(z_{i}|x_i,\theta^{(t)})]\end{split} \] 约去后项

对于$\sum_{z_{2},...z_{n}}\prod _{i=2}^np(z_{i}|x_i,\theta^{(t)})$ ,实际上它等于1：

如同$z_{1}$ 一样，$p(z_{i}|x_i,\theta^{(t)})$ 只与$z_{i}$ 相关，所以上式展开将变为：

\[ \begin{split}&\sum_{z_{2}...z_{n}}\prod _{i=2}^np(z_{i}|x_i,\theta^{(t)}) \\& = \sum_{z_{2}...z_{n}}p(z_{2}|x_2,\theta^{(t)})p(z_{3}|x_3,\theta^{(t)})...p(z_{n}|x_n,\theta^{(t)})\\&=\sum_{z_{2}} p(z_{2}|x_2,\theta^{(t)})\sum_{z_{3}}p(z_{3}|x_3,\theta^{(t)})...\sum_{z_{n}}p(z_{n}|x_n,\theta^{(t)})\end{split} \]

而$\sum_{z_{i}}p(z_{i}|x_i) =1$ ,所以全部都可以约为1。

因此$\sum_{z_{2}...z_{n}}\prod _{i=2}^np(z_{i}|x_i,\theta^{(t)}) = 1$

于是第一项将变为： \[ \begin{split}&\sum_Zlogp(x_1,z_{1}|\theta)\prod _{i=1}^np(z_{i}|x_i,\theta^{(t)}) \\&= \sum_{z_{1}}logp(x_1,z_{1}|\theta)p(z_{1}|x_1,\theta^{(t)})\end{split} \] 推广到整体

根据第一项的化简原理，化简至所有项。 \[ \begin{split}&\sum_Z[ logp(x_1,z_{1}|\theta)+logp(x_2,z_{2}|\theta)+...+logp(x_n,z_{n}|\theta) ] \prod _{i=1}^np(z_{i}|x_i,\theta^{(t)})\\ &= \sum_{z_{1}}logp(x_1,z_{1}|\theta)p(z_{1}|x_1,\theta^{(t)})+...+\sum_{z_{n}}logp(x_n,z_{n}|\theta)p(z_{n}|x_n,\theta^{(t)})\\ &= \sum_{i=1}^n\sum_{z_{i}}logp(x_i,z_{i}|\theta)p(z_{i}|x_i,\theta^{(t)})\end{split} \]

结论

通过简化后，Q函数将变为： \[ \begin{split}Q(\theta,\theta^{(t)}) &= \sum_Zlog \prod_{i=1}^n p(x_i,z_{i}|\theta)\prod_{i=1}^np(z_{i}|x_i,\theta^{(t)})\\ &=\sum_{i=1}^n\sum_{z_{i}}logp(x_i,z_{i}|\theta)p(z_{i}|x_i,\theta^{(t)})\\ &=\sum_{z_{i}}\sum_{i=1}^nlogp(x_i,z_{i}|\theta)p(z_{i}|x_i,\theta^{(t)})\\ &=\sum_{k=1}^K\sum_{i=1}^nlog[\alpha_kN(x_i|\mu_k,\Sigma_k)]p(z_{i}=c_k|x_i,\theta^{(t)})\\ &=\sum_{k=1}^K\sum_{i=1}^n[log\alpha_k+logN(x_i|\mu_k,\Sigma_k)]p(z_{i}=c_k|x_i,\theta^{(t)}) \end{split} \]

M-step

M-step目标函数： \[ \theta^{(t+1)} = argmax_\theta Q(\theta,\theta^{(t)}) \] 关于$\alpha,\mu,\Sigma$的详细求解步骤在重写这篇文章时选择跳过。因为其实我只跟着推了$\alpha$ ，均值和协方差并没有详细推（抱歉），求解$\alpha$ 时会用到拉格朗日乘子法。详细步骤请移步参考教程中的第二个连接：高斯混合模型（GMM）推导及实现

解出的最终结果：

$\alpha_k^{(t+1)} = \frac{1}{N}\sum_{i=1}^n\gamma_t(z^{(i)}_k)$

$\mu_k^{(t+1)} = \frac{\sum_{i=1}^n[\gamma_t(z^{(i)}_k)x_i]}{\sum_{i=1}^n\gamma_t(z^{(i)}_k)}$

$\Sigma_k^{(t+1)} = \frac{\sum_{i=1}^n\gamma_t(z^{(i)}_k)(x_n-\mu_k)(x_n-\mu_k)^T}{\sum_{i=1}^n\gamma_t(z^{(i)}_k)}$

GMM总结

GMM聚类流程

step1：

定义高斯分布个数K，对每个高斯分布设置初始参数值$\theta^{(0)} = \alpha^{(0)},\mu^{(0)},\Sigma^{(0)}$ 。一般第一步不会自己设置初始值，而是通过K-mean算法计算初始值。

step2 E-step：

根据当前的参数$\theta^{(t)}$ ,计算每一个隐变量的后验概率分布$\gamma_t(z^{(i)})$。

$\gamma_t(z_j^{(i)}) = \frac{\alpha_j^{(t)}N(x|\mu_j^{(t)},\Sigma_j^{(t)})}{\sum_{k=1}^K \alpha_k^{(t)}N(x|\mu_k^{(t)},\Sigma_k^{(t)})}$

step3 M-step：

根据E-step计算出的隐变量后验概率分布，进一步计算新的$\theta^{(t+1)}$